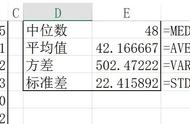
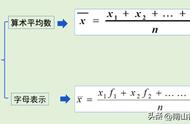
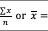相对于平均数，中位数在统计学中很多时候具有更高的参考意义。因为在很多情况下，平均数的意义并不大。例如如果有10个人，其中9个人每人月收入1块钱，而马云一人收入991块钱，那么，平均收入是100块钱。而中位数则是1块钱，所以光看平均数的话，在这种情况下意义不大。

我们首先来看一下中位数的定义：

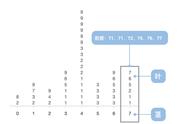
对于一个排序好的数列，如果数据总数为奇数的话，那么中位数就取最中间的一个；如果数据总数为偶数的话，那么中位数就取最中间两个数的平均值。

那么如何求出中位数呢？这个问题本质上是一个排序问题，求中位数通常有以下几种方法：

1、对数据进行排序，然后直接取出中位数，该方法时间复杂度为O(N*logN)；

2、对N个数，构建N/2大小的堆，然后遍历完所有的数再取出堆顶就是中位数了，时间复杂度为O(N*logK)其中K代表是的构建堆的大小；

3、BFPRT算法，用来求解Top-K问题。然后中位数就是求第N/2的数，即中位数。最坏时间复杂度为O(N)。

但是简单的算法在大数据应用中，很多时候并不能直接使用，因为大数据本身是一个量变引起质变的问题，数据量大的时候，要考虑的因素就更为复杂。

例如说，如果我们要解决以下的问题：

在一个大文件中，有10G个数，乱序排列，要求其中位数。应该如何做？

对于大数据来说，需要考虑的问题包括以下几点：

1、内存大小的约束，对于10G个数来说，数据量是大于很多计算机内存的，因此，如果内存不够大的话，就不可能将所有数据加载进内存进行排序；

2、数的类型约束，对于海量数据来说，其来源很多时候并不单一，特殊数据的情况也会经常存在，例如Java的整型数最大值为2147483647，而在海量数据中，很有可能出现比该数大的值，这种情况下，如果采用整型数的话，无疑会出问题。这时候就需要考虑使用长整型或者java.math.BigInteger来进行处理了。除此之外，一些来源的数据会因为各种原因，产生诸如undefined（未定义）或者是infinite（无穷大）等用字母表示的数据，这种情况如果不处理的话，程序也会产生问题。

好了，在考虑到以上问题之后，我们简单介绍一下大数据条件下，求中位数的常用方法。

一、堆排序（转化为Top-K问题）

对于Top-K来讲，不需要对数据进行排序，只需要拿新数据与堆顶数据进行比较即可，也不需要将全部数据加载到内存，只需要构建一个K大小的堆。当读取的新元素比堆顶元素小时舍弃，比堆顶元素大时替换掉堆顶。

因此，我们可以根据实际的内存大小，例如说内存只有2G的话，可以先构建一个1G的堆，得到第1G大小的元素，然后依次类推，直到求出中位数。

但是这种方法需要多次遍历数据，产生频繁的磁盘IO操作，效率很低。

二、桶排序

可以将数据根据数据类型，从小到大划分为若干个桶，例如说10000个，然后将数据根据内存大小，划分为适应内存大小的组，依次读入。例如首先装载前1G个数，遍历这些数，将它位扔进对应的桶里。

当所有数据都遍历完之后，从最小的桶计数开始类加，直到加到全部数据的一半，得到中位数。

该方法需要遍历两次数据，效率较高。

三、BFPTR算法

BFPTR算法是由Blum、Floyed、Pratt、Tarjan、Rivest五个人一起提出来的，其特点在于可以以最坏复杂度为 O(n)地求解top−k问题。

在BFPTR算法中，每次选择五分中位数的中位数作为pivot，算法步骤如下：

1、将输入数组的 n 个元素划分为 n/5 组，每组5个元素，且至多只有一个组由剩下的 n%5 个元素组成；

2、寻找 n/5 个组中每一个组的中位数，首先对每组的元素进行插入排序，然后从排序过的序列中选出中位数；

3、对于（2）中找出的 n/5 个中位数，递归进行步骤（1）和（2），直到只剩下一个数即为这 n/5 个元素的中位数，找到中位数后并找到对应的下标 P；

4、进行Partion划分过程，Partion划分中的pivot元素下标为 P；

5、进行高低区判断即可。

以上就是在大数据应用场景下，求中位数需要考虑的约束问题和基本实现思路。在遇到具体问题的时候，还需要具体问题具体分析，灵活多变的解决实际应用问题哦。