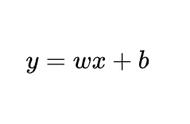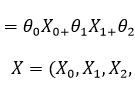基于之前我讲解的,这篇文章详细讲解下最小二乘法求解线性回归
首先来说下线性回归的定义:就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候,就能够预测出一个简单的值。
好多不懂算法的朋友,都说算法是个黑盒,那我们就假设线性回归算法是个黑盒,其实这个黑盒就是我们要求的线性回归函数,那接下来我们就求解这个黑盒子吧
在初中我们都学过一次函数y=kx b,其实这就是最简单的一维线性函数的公式,我们要求出k和b,那么这条直线就求出来了,只是求解的方法可能和初中我们学过的求解方法不一样
1.预测函数
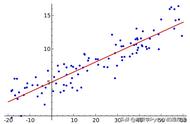
举个列子来说,我们想求解房屋面积和房屋价格的关系,这是一个典型的线性回归的例子,图上的点是训练数据,我们要拟合一条直线,来找到面积和房价的关系,这条直线就是线性回归的预测函数,也就是y-kx b

那可能有多种拟合的方法,那哪一条直线是最好的呢?这就是线性回归要求解的问题

2.损失函数
那既然是这样,肯定要有一个评判标准,那这个评判标准很简单,只要算一下实际房价和预测房价的差值就可以了,可以用两点之间的距离来表示,当我们把所有距离做加和,就能量化出预测房价和真实房价之间的误差了如下图表示

那用公式表示其实就是欧式距离的加和,其中y(i)表示的是实际房价,y^(i)表示的是预测房价