1年级
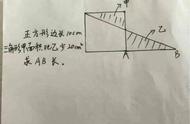
黑兔、灰兔和白兔三只兔子在赛跑。黑免说:"我跑得不是最快的,但比白兔快。"请你说说,
( )跑得最快,( )跑得最慢。
2年级
在一条长50米的公路两边植树,每隔10米种一棵,两端都种,这条路上共种多少棵树?
3年级
桌子上放着35根火柴,甲、乙二人轮流每次取走1~3根.规定谁取走最后一根火柴谁获胜.如果双方采用最佳方法,先取者想要获胜,应该先取__________根.
4年级
用红黄绿三种颜色的彩旗布置会场,要插放一排10面彩旗,要求红黄绿三色彩旗都有,并且使任两面相邻的彩旗颜色都不同,问:共有多少种摆列方法?
5年级
恰有20个因数的最小自然数是多少?
6年级
将七位数"1357924"重复写287次组成一个2009位数"13579241357924…"。删去这个数中所有位于奇数位上的数字;按上述方法一直删除下去直到剩下一个数字为止,则最后剩下的数字是( )

本期答案
1年级
解析:灰兔跑的最快,白兔跑的最慢。
2年级
解析:在一条长50米的公路两边植树,我们先考虑一边种了多少棵,每隔10米种1棵,两端都种,50米里面有5个10米,也就是说中间的间隔有5个,那么一边就可以种6棵树,一边种6棵树,两边就是6 6=12(棵)树.
3年级
解析:先取者取3根,留给后取者4的倍数根,之后与后取者凑4即可获胜。
4年级
解:首先计算,能使得任意两面相邻的彩旗不同颜色的方法数,第一面能选3种颜色中的任一种,第二面放两种剩余颜色的彩旗之一,第三面放不同于第二面颜色的两种颜色的彩旗之一。以此类推,求得方法数等于3*2*2*2*2*2*2*2*2*2=1536.在得到的数目中需除去只放两种颜色彩旗的方法数。这种方法的数目等于6.(红黄,红绿,黄红,黄绿,绿红,绿黄)
所以总共的方法有1536-6=1530.
5年级
解:因为20=2×10=4×5=2×2×5,因此,具有 20个因数的自然数是 3与9个2
的乘积,即:3×2×2×2×2×2×2×2×2×2=1536;或者是3个3与4 个2的乘积,
即: 3×3×3×2×2×2×2=432; 或者是3,5 与4个2的乘积,即: 3×5×2×2×2
×2=240,因此最小的为 240.
6年级
解析:这样删法,第一次留下了所有2的倍数位置上的数
第二次留下了所有4的倍数位置上的数
……
第N次留下了所有2^N次倍数位置上的数
显然,在2009以内的2^N,使N最大的有2^10 = 1024
因此最终剩下的是第1024位上的数。
1024 ÷ 7 = 146 …… 余2
相当于第二位上的数,也就是3。