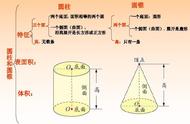
圆柱与圆锥问题作为立体图形的基本知识点,很多学生感到晕乎乎。
1.“切”
〔问题〕把一根圆柱体木材锯成相等的4份,
需要锯几次可以?
①可以横切,分两段切一刀,增加两个底面大小的面,分三段切两刀,增加4个底面大小的面,以此类推。
②还可以沿直径纵切,增加两个长方形的面,长和圆柱的高相等,宽和直径相等。
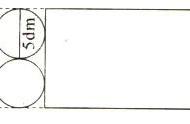
2、“刷”
〔问题:〕针对这一圆木组合,刷油漆要刷多少?
给圆木涂油漆求涂漆面积的时候需要用表面积的知识。
直接算出,还是想一下有什么简便的计算。
①如果是柱子时,只刷侧面。
②如果是个木桩,只涂一个侧面和一个上面。
③如果是个圆木料,可涂整个表面。
一个“刷”,刷出了与表面积有关的符合实际的有价值的问题,培养了学生灵活运用所学知识解决实际问题的能力。
(单位换算、转化的数学思想)
3、“削”
圆柱容球计算球体积。
〔问题〕除了对圆木“涂”“切”以外,有同学说还可以“削”成一个最大的圆锥。那怎样“削”才算是最大呢?你能用四句话说出它们之间的关系吗?
等底等高的圆柱和圆锥:圆柱体积是圆锥体积的3倍,圆锥体积是圆柱体积的三分之一,圆柱体积比圆锥体积多2倍,圆锥体积比圆柱体积少三分之二。
〔教师引导:〕如果圆柱和圆锥等底等积,那你能说出它们之间的关系吗?
圆柱和圆锥等底等积:圆柱高是圆锥高的三分之一,圆锥高是圆柱高的3倍。
如果圆柱和圆锥等高等积,那你能说出它们之间的关系吗?
圆柱和圆锥等高等积:圆柱底是圆锥底的三分之一,圆锥底是圆柱底的3倍。

学会思维导图