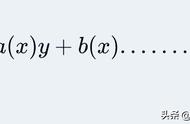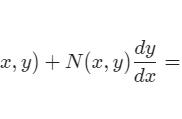二阶微分方程的一般形式
P(x,y,y',y")=0
稍微特殊一点y"=(x.y,y')
一、二阶常系数线性齐次微分方程的标准形式
形如 y" py' qy=f(x)
我们叫做二阶常系数线性微分方程
线性的要求:y,y',y"都是一次项,不含有它们的乘积项
常系数的要求:p,q都是常数。
二阶常系数线性非齐次方程:y" py' qy=f(x)
二阶常系数线性齐次方程:y" py' qy=0
y"-5y' 6y=xe^2x是非齐次方程;
y"-5y' 5y=0是相应的齐次方程。
二、二阶常系数线性微分方程的解的结构
1.解的叠加
定理:如果函数y1与y2是二阶常系数线性齐次微分方程的两个解,则y=C1y1 C2y2也是方程的解,其中C1,C2是任意常数。
y" py' qy=0
(C1y1)" p(C1y1)' q(C1y1)=0
(C2y2)" p(C2y2)' q(C2y2)=0
(C1y1 C2y2)" p(C1y1 C2y2)' q(C1y1 C2y2)=0
思考:y=C1y C2y是不是方程y" py' qy=0的通解?其中C1,C2是任意常数
例:y" y=0 y1=sinx y2=2sinx y2=cosx
y=C1sinx C2•2sinx=(C1 2C2)sinx
y=C1sinx C2cos• x
注:定理8-1说明线性齐次方程的解具有叠加性。叠加起来的解从形式上看含有C1,C2两个任意常数,但它不一定是方程y" py' qy=0的解。
2、线性相关、线性无关
(1)判定两个函数是线性相关或无关;
若y1/y2=常数,即y1,y2成比例,则y1,y2线性相关;
若y1/y2≠常数(y1,y2不成比例),则y1,y2线性无关。
(2)判断n个函数是线性相关或无关;
下。
线性相关性、线性无关性的定义:
设y1,y2,…yn为定义区间I内的n个函数,若存在不全为零的常数k1,k2,…kn,使得在该区间内有k1y1 k2y2 … knyn=0成立,泽称这n个函数在区间I内线性相关,否则称线性无关。
例:1,cos^2 x,sin^2 x=0
1,x,x^2在任何区间(a,b)内是线性无关的,因为在该区间内,要使
k1 k2x k3•x^2=0
必须
k1=k2=k3=0
3.二阶常系数线性齐次微分方程的解的结构
1.要找到它的两个线性无关的特解y1和y2
2.通解y=C1y1 C2y2
定理8-2 如果函数y1与y2是二阶常系数线性齐次方程的两个线性无关的特解,则y=C1y1 C2y2是方程的通解,其中C1,C2是任意常数。
4.二阶常系数线性非齐次微分方程的解的结构
和一阶线性非齐次方程的解一样,即二阶线性非齐次方程的
通解=相应齐次方程的通解 非齐次方程的一个特解
y1是y" py' qy=0的通解,即(y1)" p(y1)' qy1=0
y*是y" py' qy=f(x)的特解,即(y*)" p(y*)' qy*=f(x)
则y=y1 y*是y" py' qy=f(x)的通解
所以,求解二阶线性微分方程,搜先要学习齐次方程的解法。
三、二阶常系数齐次微分方程的解法
定理8—2 如果函数y1与y2是二阶常系数线性齐次微分方程的两个线性无关的特解,则y=C1y1 C2y2是方程的通解,其中C1,C2是任意常数。
y" py' qy=0
设y=e^rx,将其带入上放出,得
(r^2 pr q)e^rx=0
因为e^rx≠0,故有r^2 pr q=0(特征方程)
特征根

四种情况推导过程此处省略

例:

解:所给方程的特征方程为 r^2 2r 1=0
解之得 r1=r2=-1
通解为 S=(C1 C2•t)e^-t
将初始条件S|t=0=4代入,得C1=4
于是S=(4 C2t)e^-t
对其求导得 S'=(C2-4-C2t)e^-t
将初始条件 S'|t=0 =-2代入上式,得C2=2
所求特解为 S=(4 2t)e^-t.