老黄一直坚持分享中考数学真题，没有得到什么经济上的利益，完全可以忽略不计。但老黄依然坚持，因为老黄除了觉得这是一件特别有意义的事情之外，还能从中找到乐趣。比如从各省市历年的中考真题中，学到新的知识点。

这是上海市中考数学的一道填空压轴题，它就涉及到一个老黄以前没有学过的知识点，可能你也没有见过。

我们规定：一个正n边形(n为整数, n≥4)的最短对角线与最长对角线长度的比值叫做这个正n边形的“特征值”，记为λn, 那么λ6 = ______.

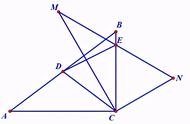
这道题考的是考生的动手探究能力，首先你要读懂题目的要求，要求的是正六边形的特征值，也就是正六边形最短的对角线与最长的对角线长度的比值。解决这个问题，必须作出图形，因为有图有真相嘛。

从上图，我们可以发现正六边形只有两类对角线，一类如BF，它是相隔一个顶点的两个顶点间的对角线；另一类如BE，它在六边形的一条对称轴上。这是正六边形的旋转对称性决定的。不难看出BF<BE，因此BF就是这个正六边形的最短对角线，而BE是最长的对角线。不过靠肉眼判断不严谨，我们可以在下面的分析中用数学的方法确定，并不需要专门证明。

正六边形的内角等于120度，因此∠A=∠AFE=∠DEF=120度。这三个角在下面的分析过程中都要用到。又正六边形的每条边都相等，所以三角形ABF是等腰三角形。

在等腰△ABF中, ∠AFB=(180度-∠A)/2=30度。因此∠BFE=∠AFE-∠AFB=90度。也就是说三角形BEF是直角三角形。

又BE平分角DEF，所以∠BEF=∠DEF/2=60度。因此λ6=BF/BE=sin∠BEF=sin60度=二分之根号3.

这道题告诉我们什么是正n边形的特征值，并且引导并教会我们求正六边形的特征值。根据这个知识，我们还可以尝试求正四边形，即正方形，或者正五边形、正七边形等的特征值。如果你能像老黄一样从学习题目中找到乐趣，又何愁学不好数学呢？

更多相关：