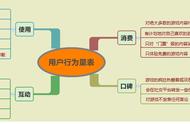
微积分先谈谈积分。我们把积分理解为用极限方法求得的曲线下的面积。如果已知一个正值连续函数y=f(x)，例如y=x²或y=1＋cosx，我们考察这样一个区域，

计算这个阴影面积A.显然，这样的区域不能分解为矩形或三角形，因而它的面积没有一个可以明显计算的直接表达式。

但是，我们可以求A的近似值。我们把从x=a到x=b的区间分割为许多小区间，并把曲线下的每个小长条用矩形代替。这些矩形面积的总和S给出了A的一个近似值。

如果令分划数为n，显然矩形的个数越多，宽度越小，则近似值就越接近A。

Sn→A，

我们就把由这个极限过程表示的区域的面积A定义为函数f(x)由a到b的积分，用专门的积分号表示，可写成

符号∫，dx和“积分”，都是莱布尼兹为了提示获得极限的方式而创立的。

Xj为分划点

莱布尼兹用∫代替求和符号∑，并且用符号d代替差的符号△，从而把近似的和式趋于A的极限过程符号了。