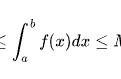积分第一中值定理，是作为习题出现在同济第七版总习题五中的。这个定理其实是积分中值定理的推广形式，既然名字中有个第一，那就说明还有别的推广形式。以后也会发出来。

这个定理的证明与之前发过的证明方法上基本一致，最后都是通过介值定理的推论找到“可赛”那一点。

上图的证明过程中，g（x）<0时的具体过程我没有写，与g（x）>0时基本一样。略有不同的地方在于，中间不等号变向过两次，然后又回到g（x）>0时的最后得出的形式。有兴趣的朋友可以自己试试推导下。

多说一句，这种基本定理的证明是我个人最喜欢做的。我感觉，每一个定理都有一种质朴的美感，它们数学发展历史上一座座里程碑，自己推导一下，就像踏着先贤的足迹重游，感觉很好。