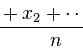选自 Fahd Alhazmi's Blog

作者：Fahd Alhazmi

机器之心编译

参与：魔王、杜伟

本文将对标准差这一概念提供直观的视觉解释。

本文作者为纽约市立大学在读博士生 Fahd Alhazmi，专注于神经科学、人工智能和人类行为研究。

统计学中最核心的概念之一是：标准差及其与其他统计量（如方差和均值）之间的关系。入门课程中老师常告诉学生「记住公式就行」，但这并非解释概念的最佳方式。本文将对标准差这一概念提供直观的视觉解释。

假设你有一个成绩单，在本案例中这即是现实测量（real-world measurements）。我们想将这些测量中的信息「压缩」为一组量，以便后续对比不同班级的成绩或不同年份的成绩等。鉴于认知能力有限，我们不想挨个查看分数，来找出平均分更高的班级。这时就需要总结数字，描述统计学就派上用场了。

总结数字的方式有两种：量化其相似性或差异（difference）。

• 量化数字的相似性即「集中趋势量数」（measures of central tendency），包括平均数、中位数和众数；
• 量化数字的差异即「差异量数」（measures of variability），包括方差和标准差。

标准差揭示一组数字中彼此之间的差异，以及数字与平均值之间的差异。

举例而言，假设你收集了一些学生分数（出于简洁性考虑，我们假设这些分数是总体）。

我们首先在简单的散点图中绘制这些数字：

绘制完成后，计算差异的第一步是找出这些数字的中心，即平均值。