我们都会犯错。有时候,如果你处理得当,它们可以成为宝贵的学习机会。它被称为“人为错误”是有原因的;即使是我们当中最优秀的人,也会时不时地漏掉一个“t”或一个“i”。这就是生活。
首先找出问题出在哪里通常是一个好主意。
错误的大小是一个关键的细节。你偏离目标的程度有多严重?是侥幸脱险还是大错特错?
当你期望的值和你实际得到的值之间存在差异时——你用数学百分比来表示这种差异——这被称为百分比误差。计算百分比误差涉及比较期望值和实际值,以确定现实与理论期望的偏差程度。
今天,我们将揭开正确报告百分比误差的神秘面纱,并向您展示如何在现实生活中使用它。
百分比误差公式是什么?
这个方程再简单不过了。下面是:
百分比误差= |实验值-实际值| /实际值x 100%
您最初预测的值有许多名称,包括精确值,接受值,估计值,理论值,近似值或实验值,这取决于上下文。例如,一个物理专业的学生计算速度时,会参考一个基于速度公式的可接受值,但在她的实验中,速度的近似值或测量值可能不同。在另一种情况下,企业所有者在预测收入时可能会参考估计值。
类似地,您的实际结果有多个标签,包括实际值、测量值和精确值或已知值。不管你怎么称呼它,实际数字背后的精神是一样的。
有些人发现书面说明比数学公式更有用。如果你是其中之一,别担心。以下是百分比误差计算的逐步演练:
·第一步:用实验值减去实际值。这被称为相对误差。
·第二步:取你在第一步中得到的数字的绝对值(这就是两条竖线所表示的)。这个新数字被称为绝对误差,它确保你的最终百分比不包含负号。
·第三步:将该数字除以实际值。
·第四步:将结果乘以100。
·第五步:写出你的最终答案。
如何计算百分比错误的例子
现在我们准备将百分比误差公式用于试驾。
示例1
假设你是一个书呆子,即将迎来一个长假。你去图书馆找一些阅读材料。在你打开前门之前,你假设你要看三本书。但是,不管出于什么原因,你只带了两本书回家。你估计的误差百分比是多少?
在我们的例子中,实验值为3,实际值为2。代入这些数字,你会得到:
百分比误差= (3 - 2)/2 × 100
我们猜你已经知道3减2等于1。这给我们留下了:
百分比误差= 1/2 × 100
1除以2,得到如下结果:
百分比误差= 0.5 × 100
100乘以0.5等于50。但是记住,我们必须用百分比来表示最终答案。当我们这样做时,我们知道你最初的猜测有50%的误差。
这个例子完全是关于数量的(例如,图书馆图书的数量)。但是,百分比误差公式也可以应用于许多其他值,比如速度、距离、质量和时间。
记住这一点,我们再看一遍公式。
示例2
假设一个大学运动员认为他需要45秒来完成一项硬核训练挑战。但当他进入健身房时,这套动作只需要60秒就能完成。他开始时估计的时间误差百分比是多少(45秒)?
百分比误差= (45 - 60)/60 × 100
马上,我们就遇到了一个难题。如果用45减去60,就得到一个负数(确切地说是-15)。
用-15除以60得到-0.25,这是另一个负值。我们不能止步于此;我们还需要用-0.25乘以100,得到答案-25。这是否意味着误差百分比是-25%?
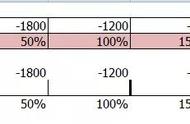
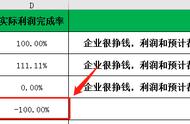
估计值与实际值之间的误差百分比不能表示为负值。它总是写成正值,不管开始的估计是太大还是太小。
这就是我们的老朋友“绝对误差”和“相对误差”发挥作用的地方。-15的值只是相对误差。在继续计算之前,你需要取它的绝对值。一旦你的绝对误差是15,你可以把它除以60,再乘以100,得到25%的百分比误差。