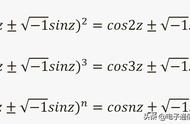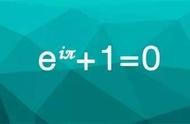这期来谈谈数学方面的话题。欧拉公式被誉为“最美数学公式”，它把e（自然对数的底）、π（圆周率）、i（虚数单位）、整数0和1联系在一起。

笔者第一次见到这个式子是在科普读物上。当时最为困惑的一点就是，πi是纯虚数，e的πi次方怎么就变成了一个实数？e、π两个看似无关的数学常数为何神奇地通过虚数单位i联系在一起？

事实上，上面提到的公式只是原始欧拉公式的特殊情况，其原始形式如下图所示。表面上看，它似乎提供了计算“纯虚数次方”的方法。要正确理解欧拉公式，就有必要先理解“虚数次方”的概念（“虚数”默认指纯虚数，下同）。

↑↑欧拉公式的原始形式

一个数的“多少次方”的概念最初只对正整数幂次才有意义。a的n次方（n为正整数）就是n个a相乘：a×a×a×…×a。在不引入新定义的情况下，若n不是正整数，a的n次方就无意义。例如，我们尚不明确“-3个a相乘”或是“1.23个a相乘”的含义。

在数学中，我们之所以能计算非整数次方，是因为人们对定义做了拓展，这带有人为规定的性质。当然，拓展遵守一个原则：尽量使拓展前的数学性质在拓展后仍适用，类似于软件的“前向兼容性”。此外，作为新定义，拓展必须建立在已有的定义上，否则就会有模糊性。

作为例子，我们来看看“a的n次方”（简记为a^n）中的n是如何拓展到负整数的：n为负整数时，记n的绝对值为|n|，则a^n等于a^|n|再取倒数。这一拓展满足“前向兼容性”，例如(a^n)×(a^m)=a^(n m)这个性质在拓展后仍适用；拓展中的绝对值、倒数运算都是已定义的，没有模糊性。这样看，这个拓展是非常自然的。最终，我们把n推广到了任意实数x。

那么，我们能否把实数x拓展到虚数情况？为了契合主题，这里只考虑e^x。要以“较为自然”的方式把x拓展到虚数，可以考察e^x的幂级数形式，如下：

似乎把上式的x简单代换为ix，拓展工作就完成了。但要注意的是，e^x原本是定义在x为实数的情况下，因此上式只对实数情况适用，把x简单替换为ix得到的“等式”必须理解为仿照e^x幂级数形式人为规定的定义式。

在上图中，我们特别在等号上加“def”以强调它是定义式。我们可以把等号右边每一项计算出来，然后把实数部分和虚数部分各自合并，如下图。

↑↑ e^(ix)的正式定义

我们把上式作为“e的虚数次方”的正式定义。它的右边只涉及乘除运算、正整数次方以及无穷级数求和，因此建立在已有定义上。定义式中括号部分刚好就是余弦、正弦函数的级数形式，从而自然地导出了欧拉公式！利用这点，我们可以证明仍有e^(ix)×e^(iy)=e^(ix iy)，因此这个定义也满足一定“兼容性”。

根据这些讨论，欧拉公式是e^(ix)的定义式的简单推论。不难看出，e的“虚数次方”与e的实数次方在定义上有很大差别。此外，“虚数次方”与实数次方并不是完全兼容，比方说，实数情况下有a≠b就一定有e^a≠e^b，这个性质在虚数情况下不适用，一个简单例子是e^(πi)=e^(3πi)。因此，“虚数次方”并不是好的说法，e^(ix)只是一个形式记号。在一定意义上，e^(ix)是cos x isin x的简便记法。