今天为大家带来高中数学的知识点，希望大家能够好好记住，一次考过!

1.数列

数列这一模块常考特殊的数列，而不是简单的等差等比数列。所以特殊数列的通项公式以及前n项和的求和方法是复习的重点。

如13年下半年考了1道数列的选择题，已知一元二次形式的数列通项公式，求该数列的最小项。还有15年下半年也考了1道选择题，判定两个特殊数列的不等关系。

2.不等式

不等式在选择题解答题中都会出现，其中选择题常考指数、对数等一般的数的大小比较，这样的题通过运用函数的知识很快能解决，解答题中主要是关于不等式的证明，这样的题难度就较大，如13年上半年就考了1道定义数列不等式的证明。

3.矩阵的相关概念及计算

矩阵的考察频率非常高，几乎年年考。具体的考点是矩阵的简单运算、矩阵变换下的曲线方程、正交矩阵的判定、矩阵的特征向量特征值、矩阵的变换等。

4.线性方程组

线性方程组是高等数学的一大重点内容，常考齐次，非齐次线性方程组的解，以解答题的形式出现。如，12年下半年考了1道求齐次线性方程组的解，并求方程组解的维数；15年下半年考了1道非齐次线性方程组，要求证明方程唯一解存在时，几个向量线性无关。

5.正态分布

正态分布的考点较少，考生重点复习满足条件概率的计算。

6.导函数的应用

导函数的应用常考导函数的几何意义、函数的极值的计算、函数的切线方程、高次函数零点等。如13年下半年考了1道几何意义题、12年下半年第1道选择题，让求三次函数图像与x轴交点的个数。

7.函数的连续性、可导性

函数的连续及可导性常以选择题形式出现，考题的难度不大，会判定函数的连续性和可导性即可。如12年考的就是分段函数在分界点处的连续性和可导性。

8.极限

这一知识点常考数列和函数的极限计算，如13年上半年选择题第1题就是考数列和函数的极限，16年上半年考的是求函数的极限。

9.定积分

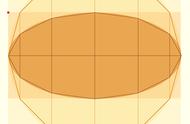
定积分常与函数综合在一起考察，具体考的是定积分函数的导函数，以及定积分的几何意义。如13年上半年1道选择题是求定积分函数导函数零点的个数;又如13年上半年解答题考的是利用定积分求椭圆所围成图形的面积。

10.中值定理

罗尔中值定理、拉格朗日中值定理的证明考察的频率还是相对比较高的，如13年和15年下半年均考到了拉格朗日中值定理的证明，并简述其与中学教学内容的关系。

11.曲线、曲面方程

空间曲面、曲线方程考察的频率非常高，常考切平面、切线方程、以及曲面、曲线方程，在选择题，解答题都会出现。如12年下半年考了曲面的切平面方程;14年下半年考了根据参数方程写曲线的一般方程；13年上半年和15年下半年均考了旋转曲面的方程;16年上半年考了根据方程确定的二次曲面类型。

12.逻辑关系

逻辑关系主要就是考四大命题、四种条件关系，而且只出现在选择题当中，所以难度不大，要特别注意否命题的判定。如12年下半年考了命题的否定，14年下半年考了充要条件。

13.空间线面、面面关系

空间线面、面面关系也是常考的考点，其中空间线面关系就考过，如14年下半年就考了空间直线与平面位置关系，并要求线面夹角。

14.概率

概率题在选择和解答题都会出现，不过这部分题难度不大，如目前考过简单的掷硬币、摸球概率计算，解答题考过两个事件的关系的证明。如12年下半年就考了1道两独立事件的证明。

15.圆锥曲线

圆锥曲线中椭圆、双曲线、抛物线均考过。常考这些曲线围成一定图形的面积、曲线方程。如13年上半年考了2道，分别是双曲线方程的判断，以及抛物线的切线与x轴交点横坐标解析式。

16.无穷级数

无穷级数常以选择题形式考察，其中求函数级数的收敛区间是最常考的知识点。如15年下半年考了函数级数的收敛区间，16年上半年考了不收敛的函数级数。

17.教学原则

数学教学原则这一块，连续3次考了严谨性与量力性教学原则，所以教学原则这一块希望广大考生要引起重视。

18.数学知识的教学及数学史

数学知识这一块考的比较多也很泛，目前考过“同化”数学概念的作用、数学知识的定义，选修1的内容、案例分析会考编制专业数学题目。数学史这一块常考相关数学知识的创始人，如目前考过微积分、勾股定理的创始人。

19.数学课程标准

义务教育数学新课标和高中数学课标均是常考点，还会结合案例分析进行考察。其中课标中的一些基本理念是最常考的，其次是具体的数学专业内容，教学评价等。如目前考过教师的引导作用、高中课程引入二分法的意义、对学生的评价、评价主体、书面测验、课程总目标、高中课标中五种基本能力。

20.教学设计

最后是教学设计这一块，资格证教学设计的考察不同于教师招聘考试，通常要求就某一课题进行相关题目的编制，教学目标、教学重难点、教学过程的撰写，也会考对已知课题教学目标、教学重点的分析。

如13年下半年已知“函数概念”的教学目标，根据目标设计实例并说明意图，说明与初中函数概念的不同，撰写本课的教学重难点，14年下半年考了关于教学目标的分析与编写，15年下半年是已知“不等式”的两种教学重点方案设计，问赞同哪一个，给出不等式的几何解释、从几个维度谈谈对不等式数学知识的认识。

|来源：网络综合|声明：如本文内容涉及版权问题，请及时与我们联系，感谢分享