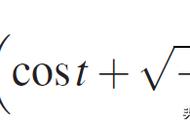古代三大几何尺规作图问题分别是三等分任意角,立方倍积和化圆为方。科学家们已经证明了,用尺规作图是无法解决的,前两个问题是要对一个数开立方,后面的一个要做出圆周率,而尺规作图只能做出有限次数的加减乘除和开平方,无法达到目的。
远在十八世纪中叶,荷兰数学家雅各布(Jacob de Gelder)提出了一个近似的化圆为方的做法,精度很高,本文就讨论一下。我们知道,南北朝时期的数学家祖冲之计算出了圆周率的密率355/113 = 3.1415929….,这是个有理数,可以用尺规作图实现,而且跟圆周率很接近,精确到小数点后第六位,也就是百万分之一,对于应用层面来讲,完全够用了。具体做法如下图:

尺规作图过程简述
步骤如下:
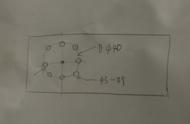
1. 已知圆的半径为1,作相互垂直的直径AB和CD,在CD上取一点E,使得CE=7/8。
2. 连接AE,在AE上取一点F,使得AF=1/2。
3. 通过F作AB的垂线交AB于G。
4. 连接EG,并通过点F做EG的平行线,交AB于点H。
5. 延长AB,并作BJ=CB,以及JK=AH。
6. 以AK为直径作圆,交CD的延长线于M。
7. 以BM为边做正方形,该正方形即为所求。
证明如下:因为FG平行于CD,所以三角形AFG相似于三角形AEC,从而AF/AE=AG/AC——①
因为EG平行于FH,所以三角形AFH相似于三角形AEG,从而AF/AE=AH/AG——②
两个式子相乘,得到(AF/AE)^2=AH/AC,由于AC=1,AF=1/2,而AE^2=AC^2 CE^2,故AH=:

因此AK=3*AC JK=3 16/113=355/113。
又因为以AK为直径的圆L交CD的延长线为M,则三角形AMK为直角三角形,则根据射影定理:CM^2=AC*CK=AK-1,则BM^2=CM^2 CB^2=AK-1 1=AK,因此作BM为边的正方形,面积等于AK=355/113,接近于圆周率,就是近似的化圆为方。精度为亿分之一,大约是半径100公里的圆,正方形的边长误差为7.5毫米。