不经过圆心要怎么才能把披萨平分呢？就是这么一个看似简单的分披萨问题，却困扰了无数数学家40多年的时间。

1967年一个名叫L.G.厄普顿的人在数学杂志上提出了这样一个问题——“披萨最常见的切法就是通过披萨的圆心任意切N刀，这么切披萨总能被等分，但是要是第一刀没有切在圆心上，我们还能完美的等分披萨吗？”在这个几何问题发表在杂志上后，世界各地的数学家们就开始了对它的研究。

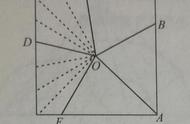
随着研究的深入，大家发现这个问题远没有想象中的那么简单。经过一年的努力，数学家迈克尔•‬哥‬德堡对这个问题进行了解答，但是他的解答仅限于切了四刀、六刀、八刀这样的偶数刀的情况，并且它的推导与证明过程普通人三天三夜也不一定能理解的通透。到了1994年，数学家拉里•卡特和斯丹•瓦根‬用割补法裁‬了无数个圆，吃了无数个披萨，对切四刀情况下的问题，给出了一个初中生也能看懂的直观图解，证明经过打乱*。可以发现，在每‬刀与另外一刀‬的夹角是45度的情况下，无论是否经过圆心，披萨总会被等分成两份。