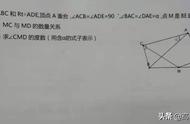
三角形的中位线证明一直是初中几何性质定理证明的难点，既要证明数量关系，又要证明位置关系。而证明突破口就在于能否根据中点添加相应的辅助线，证明的方法虽然多，但是万变不离其宗，都是围绕中点的性质进行展开。

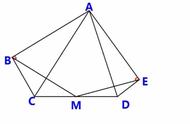
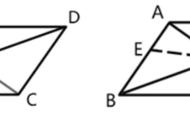
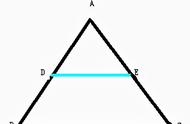
背景条件：在三角形ABC中，D、E分别为AB、AC的中点，联结DE。试探索DE与BC的数量关系与位置关系。

一、倍长中线添加辅助线

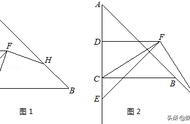
证法1（图1）和证法2（图2）借鉴了教材引入中的剪拼法，利用中点的对称性添加辅助线，得到全等三角形，通过全等三角形及平行四边形性质，得到DE与BC的数量关系及位置关系。

二、利用中点，构造平行四边形

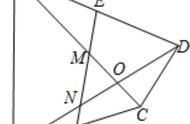
证法3（图3）和证法4（图4），通过添加平行线，利用中点构造平行四边形，再根据全等三角形性质和平行四边形的判定和性质，得到DE和BC的数量关系和位置关系。

三、利用面积法证明