人工智能数学基础系列文章
- 1. 人工智能数学基础----导数
- 2. 人工智能数学基础----矩阵
- 3. 人工智能数学基础----线性二阶近似
人工智能的学习对于数学要求还是需要一定的功底的,不管是算法还是涉及到的名词概念,都是建立在数学模型的基础上来做训练学习的,所以非常有必要把涉及到的数学知识都理解和梳理一遍,才能把思维从传统的编程方式转变过来。
这里介绍的是 一元函数(标量场)的导数,以后会介绍多元函数(矢量或者多维矩阵场)导数,因为多元函数需要向量和矩阵相关的知识,会先介绍向量和矩阵相关之后,再来详细介绍多元函数导数问题
一、导数
1. 定义
函数导数f'(x0),就是函数f(x)在x0值处的导数,也是函数f(x)在x0这个点的切线斜率,这个点我们这里用P点表示,如图:

2. 求导的推导过程
我们知道高中的时候对于函数斜率的计算公式:y-y0 = m(x - x0),其中m就是函数的斜率。具体我们要怎么求出这斜率值或者导数呢。

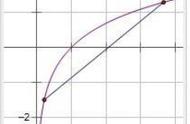
上图中,假设有一条直线l,与函数f(x)相交于p0和Q点,保持p0点不变,当Q点沿着函数f(x)向p0点无限靠近,P0点和Q点重合的时候,此时直线l就和P0的切线n重合,这是一个极限的无限趋于x0值(也就是P0点)的求解过程。 上图看出,P0点到Q点在x轴上的变化量是Δx,Q点的x值就是x0 Δx,Q点在y轴上的变化量就是Δy,或者叫Δf。P0和Q点的坐标是:P0( x0, f(x0) ),Q( x0 Δx, f(x0 Δx) ) 最开始我们提到了,斜率的计算公式y-y0 = m(x-x0),m = (y - y0) / (x - x0),m = Δf / Δx, 这是割线l的斜率,要求P0的斜率,则要引入极限的概念,斜率或者说导数的如下(当Δx趋近于0的时候,也就是变化量趋于0的时候,Q点和P0点重合):

3. 求导例子
例子一
根据以上公式,举个例子,有函数f(x) = 1/x,求在x0上的导数?