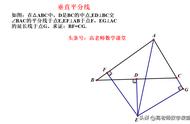
1.等腰三角形的顶角平分线或底边的中线垂直于底边（等腰三角形的高线、中线与角平分线重合，即“三线合一”）

2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。（反过来也成立，如果一个三角形是直角三角形，那么这个直角三角形斜边上的中线，等于斜边的一半）

3.在一个三角形中，若有两个角互余，则第三个角是直角。（如果角A和角B的和为90度，那根据三角形内角和等于108度，那另外一个角一定为直角，即90度）

4.邻补角的平分线互相垂直。

5.一条直线垂直于平行线中的一条，则必垂直于另一条。

6.两条直线相交成直角则两直线垂直。（两条线之间的夹角等于90度，即可说明这两条直线互相垂直）

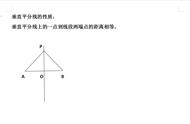
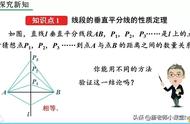
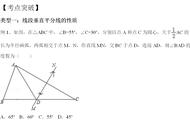
7.利用到一线段两端的距离相等的点在线段的垂直平分线上。

8.利用勾股定理的逆定理。（如果两边的平方之和，会等于第三边的平方，那么可说明这个三角形是直角三角形）

9.利用菱形的对角线互相垂直。

10.在圆中平分弦（或弧）的直径垂直于弦。

11.利用半圆上的圆周角是直角。（圆周角所对的是直径）