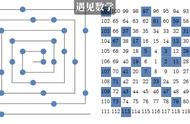
完全数( Perfect number),又称完美数或完备数,是一些特殊的自然数:它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。
举例
例如:第一个完全数是6,它有约数1,2、3、6,除去它本身6外,其余3个数相加,1 2 3=6。第二个完全数是28,它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加1 2 4 7 14=28。后面的数是496,8128等等。
例如:
6=1 2 3
28=1 2 4 7 14
496=1 2 4 8 16 31 62 124 248
8128=1 2 4 8 16 32 64 127 254 508 1016 2032 4064
相关概念对于“4”这个数,它的真因子有1、2,其和是3。由于4本身比其真因子之和要大,这样的数叫做亏数。对于“12”这个数,它的真因子有1、2、3、4、6,其和是16。由于12本身比其真因子之和要小,这样的数就叫做盈数。那么有没有既不盈余,又不亏欠的数呢?即等于它自己的所有真因子之和的数,这样的数就叫做完全数。
性质1、它们都能写成连续自然数之和
例如:6=1 2 3,28=1 2 3 4 5 6 7
496=1 2 3 …… 30 31
2、每个都是调和数
它们的全部因数的倒数之和都是2,因此每个完全数都是调和数。例如1/1 1/2 1/3 1/6=2
/1 1/2 1/4 1/7 1/14 1/28=2
3、可以表示成连续奇立方数之和
除6以外的完全数,还可以表示成连续奇立方数之和。例如:
28=13 33
496=13 33 53 7^3
8128=13 33 53 ……… 153
33550336=13 33 53 …… 1253 1273
4、都可以表达为2的一些连续正整数次幂之和
例如:
6=21 2
28=22 23 24
8128=26 27 28 29 210 211 212
33550336=212 213 …… 224
5、完全数都是以6或8结尾
如果以8结尾,那么就肯定是以28结尾
6、位数字相加直到变成个位数则一定是1,除6以外的完全数,把它的各位数字相加,直到变成个位数,那么这
个个位数一定是1。(亦即:除6以外的完全数,被9除都余1)
28:2 8=10,1 0=1
496:4 9 6=19,1 9=10,1 0=1
前12个完全数6
2…28
3……496
4…8128
5…33550336
6……8589869056
7…137438691328
8…2305843008139952128
9……2658455991569831744654692615953842176
10……191561942608236107294793378084303638130997321548169216
11………1316403645856964833723975346045872291022347231838694311778
3728128
12……1447401115466452442794637312608598848157367749147483588906
6354349131199152128
之所以只写到第12个,是因为第13个有314位,那么多数字堆在这里不美观。