等腰三角形、等边三角形、直角三角形是初中数学重点考察内容,也是学习的难点。
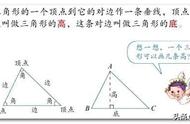
一、等腰三角形的概念 1. 定义有两条边相等的三角形叫做等腰三角形。两条相等的边叫做腰,所夹的角叫做顶角,另一边叫做底边,底边与腰形成的两个角叫做底角。
2. 性质(1) 等腰三角形是轴对称图形,底边中线是对称轴(底边的高、顶角的角的角平分线都是对称轴)
(2) 等腰三角形两个底角相等,简称等边对等角。
(3) 等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简称三线合一。
3. 判定(1) 两内角相等的三角形叫做等腰三角形
(2) 两个边相等的三角形叫做等腰三角形
二、等边三角形 1. 定义三条边都相等的三角形叫做等边三角形。
2. 性质(1) 等边三角形有三条对称轴,中线是对称轴
(2) 等边三角形三个角相等,每个角都为60º
(3) 等边三角形的顶角平分线、底边上的中线、底边上的高相互重合,简称三线合一。
3. 判定(1)三条边都相等的三角形是等边三角形
(2)三个角都相等的三角形叫做等边三角形
(3)有一个内角是60º的等腰三角形是等边三角形。
三、直角三角形 1. 定义有一个角是直角的三角形叫做直角三角形
2. 性质(1) 直角三角形两个锐角互余
(2) 直角三角形斜边上的中线等于斜边的一半
(3) 直角三角形中,30º角所对的直角边等于斜边的一半
(4) 勾股定理:a2 b2=c2(a、b为直角边,c为斜边)
3. 判定(1) 有一个角是直角的三角形,或者两个锐角和为90º的三角形为直角三角形。
(2) 一边的中线等于这条边的一半,这个三角形是直角三角形。
(3) 勾股定理逆定理:如果有a2 b2=c2(a、b、c为三角形的三个边),则三角行为直角三角形
四、基础题型 1. 例题1如图,边长为4的等边ΔABC中,D、E分别为AB、BC的中点,EF⊥AC于点F,G为EF的中点,连接DG,则DG的长为?

解:连接DE,
因为:EF⊥AC,∠C=60º
所以∠FEC=30º,
因为:ΔABC为等边三角形,DE为中位线
所以有:

(1)等边三角形及内角为60º
(2)三角形中位线
(3)直角三角形30度内角所对直角边等于斜边的一半
(4)直角三角形勾股定理
3. 解题思路和技巧DG是非常孤立的,既不是中位线,也不平行某一边,即不是三角形的某一边,也不是规则四边形的边,很难下手,因此必须画辅助线把DG融入某个三角形内,因为D、E分别是所在边的中点,连接起来是三角形的中位线,因此连接DE,尝试解题。
因为目前只学了等腰、等边、直角三角形,因此要解出一个线段DG的长度需要以下知识
(1) 等腰三角形
(2) 等边三角形
(3) 直角三角形
(4) 直角三角形斜边中线等于斜边的一半
(5)直角三角形中,30°角所对的直角边等于斜边的一半
最后通过分析角的关系,可以得出DG在直角三角形内
总结:构筑辅助线是解决一些问题的关键
五、综合题型

把ΔAEC绕A点顺时针旋转60度,AC与AB重合AE与AF重合,连接FD,做FG⊥BC,交BC于G点,AH⊥BC,交BC于G点。
因为: ,∠BAC=120º,AB=AC
所以∠ABC=∠ACB=30º
因为:ΔAFB≌ΔAEC
所以:AF=AE,∠ABC=∠ABF=30º,∠FBG=60º,∠FAD =60º
因为 :
AF=AE,,AD=AD,∠FAD==∠DAE= 60º
所以ΔADF≌ΔADE
所以: DF=DE
设FB=EC=2X
则BG=X BD=4X


1) 等腰三角形
2) 图像的旋转
3) 直角三角形及勾股定理
4) 直角三角形中30°角所对的边等于斜边的一半
5) 直角三角形勾股定理
6) 三角形全等
(3)解题思路和技巧DE在ΔADE中,但是三边关系无法确定,题目中给出了角度的关系,因此利用角度关系*三角形是思路,然后再利用三角形全等,直角三角形等解出线段DE的长度。
通过旋转图形、移动图形、折叠图形是最常用的图形组合方法,我们尝试用旋转图形法解决问题,
总结:通过移动图形、旋转图形、折叠图形进行图形组合,从而解决问题是常用的方法,应该熟练掌握。
2. 解法2旋转ΔABD进行解题
3.解法3沿AD折叠ΔABD解题
上述两种方法请读者自行尝试解题,不再叙述。