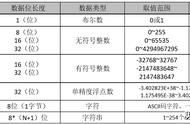
我是一个计算机专业大一的萌(lā)新(jī),刚刚开始接触二进制。很多朋友都知道计算机内部的数据通过二进制来储存和计算,但是一个小小二进制非要整一些花里胡哨(bushi)的东西,原码补码反码的一群东西,头大[石化]搞得我一脸懵。

来自渣渣的咆哮
可是又不能真的不学[泣不成声]日子再苦也得过是不是。在网上查了好多资料终于有了一点点头绪。
为什么要引入补码这个概念?我们已经知道在计算机的内部,所有的数据都是以二进制的形式存在的。但是,有一个问题,正数好说直接表示就好了,可是负数呢?计算机又存不了负号,那可咋办呢?于是人们就想出了一种表示数的模式------一种能表示出符号的二进制表示法,用最高位来表示符号,0就是正,1就是负。
以8位二进制数为例,51和-51的二进制如下(位数不足前面补0)
51=(00110011)₂
-51=(10110011)₂

瞬间就明朗了起来,但是仔细想一想还是有问题的。就是这个
(00000000)₂= 0
(10000000)₂=-0
正0和负0,啊这……有点奇怪。虽然正0和负0都是0,但是0对应着两个二进制码,这就使得二进制表示的数少了一个。仍以8位二进制为例,按照排列组合计算有256种不同的排列,可如果按照这种模式,那么它能表示255个数。所以这明显不是最优的表示模式,而且在计算的过程中可能会有别的问题(具体我也不是很了解会有啥问题,毕竟我也是小新手[尬笑])。
于是就引入了补码这个东西,而刚刚的那种带符号的表示方式被称为原码。
所以补码到底又是个啥?其实按照我的理解,补码和原码在根本上没有多大的关联。因为,补码直接就去解决最开始的那个问题:计算机无法直接储存负号,那怎么表示负数?补码就另辟蹊径,找到了另一个解决问题的思路:将负数转变为正数。

但是不是随便转化,有一个固定的方式,就是把十进制的负数加上2的n次方,n是将要转化为二进制的位数。比如求-28八位补码就用加上2的8次方,然后把和再转化为二进制。如此就避免了负数转化为二进制的问题。而正数本身就可以正常转化为二进制,所以正数的补码还是它本身的二进制。
那咋就又涉及到了反码了呢?这个问题问得好(据说自问自答的都是傻子[抠鼻]),通过加上2的n次方的方式终究太麻烦,而且不能与原码建立联系。而反码就是二者之间的桥梁,不仅能联通原码与补码,还能使原码转化为补码更加简单。在不引进反码的时候,从原码到补码的转换是通过计算的方式,而通过反码只需要在形式上的进行变化。
通过反码将原码转化为补码非常简单。符号表示法的负数二进制的反码,就是把除了最高位(符号位)的其余数位变成相反的数,原来的1变为0,0变为1。比如
(10010011)₂的反码是(11101100)₂
因为引进反码、补码都是为了解决负数的表示问题,所以正数的反码和补码都是它本身。
得到反码之后把反码加上1就得到了补码。那有的朋友可能会有些疑惑,这是为什么呢?
为什么通过上述操作能得到补码?这个问题也困扰了我很久,我试图通过数学的方式去证明它,可以证明,但是很麻烦。我前面说通过反码的渠道将原码转化为补码是一种形式上变化的方法,没错不必想太复杂,我们先回到补码的本质。
补码是十进制负数加上2的n次方在转化为二进制得到的,就有这么个式子
补码-2的n次方=原码
于是就有
原码 补码=2的n次方
这就是我们刚才操作的依据。这个2的n次方有个专业点的名字叫做模,写成数字的形式就是1后面n个0。
而反码与原码的数位刚好互补,相加就能得到一串的1(假设有n个1),那反码加一在加上原码就呢个得到1后面n个零,就是模。又因为“原码 补码=2的n次方”,所以反码加一就是补码。
举个例子(上面的例子)
(10010011)₂的反码是(11101100)₂
相加得(11111111)₂(最高位是符号位,不做加法)
反码加一得(11111000)₂
与(10010011)₂的和为(100000000)₂即2的n次方
以上大概就是原码补码与反码的前世今生了,本人水平有限,文章中可能会有一些错误,欢迎大家在评论区指正。也欢迎大家在评论区讨论。