(bluehouse456 全文整理)
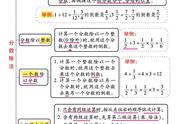
今天我们学习的内容是人教版六年级上册分数除法第一课时顺道课题,你能提出哪些问题?
我想知道分数除法的计算方法与整数除法和小数除法的计算方法一样吗?
我想知道分数除法与分数乘法有关系吗?
上节课我们认识了倒数,倒数在分数除法中有什么用呢?
同学们提出了这么多有价值的数学问题,带着这些问题进入今天的学习,相信你们一定会有很大的收获。
把一张长方形纸的五分之四平均分成两份,每份是这张纸的几分之几?
要解决每份是这张纸的几分之几,怎样列式,你是怎么想的?
让我们来听听小芳是怎么说的。
因为是把五分之四平均分成两份,求每份是多少?所以用除法计算,列式是4/5除以二。
小芳结合题意非常准确的说出了这个除法算式的意义。
4/5除以二等于多少呢?
有的同学很快就说出了等于2/5。
计算结果是不是2/5,有什么方法验证呢?
同学们先自己想一想,再试着做一做,一会儿我们来交流一下。
哪位同学想说说自己的想法?
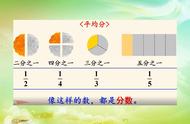
我用折纸的方法来验证。
先把这张纸平均分成五份,表示出其中的四份。
也就是这张纸的4/5,把这五分之四平均分成两份,其中的一份就是2/5。
月月就地取材,用折纸的方法形象直观的验证了4/5除以二等于2/5。
有的同学还有不一样的想法,让我们来听一听。我是这样想的,4/5里面有四个1/5,把四个1/5平均分成两份,每份就是两个1/5,也就是2/5,所以4/5除以二等于4/5除以二等于2/5。
能够想到把分数单位的个数平均分从分数单位及分数单位个数的角度进行分析,看来你对已有的知识掌握的很扎实,并且能够很好的进行迁移类推。
听了他的介绍,小明也想给大家介绍一下自己的想法。
我也想到了分数单位的个数进行平均分,得到结果,我是通过画图说明的,大家看,我先把一张纸平均分成五份,用阴影表示其中的四份,也就是4/5,把五分之四平均分成两份,就是四个1/5,平均分成两份,每份就是两个1/5,也就是2/5。所以4/5除以二等于4/5除以二等于2/5。
小婷也用了画图的方法,只不过他画的是线段图,但说明的道理和得到的结果和他们是一样的。
这两位同学,还有刚才采用折纸方法的同学,通过直观的图形,不仅能够帮助自己解决问题,而且也让我们一下子就看明白了他们的思考过程,数形结合,真是我们解决问题的好办法。
谁还想说说自己的想法?
因为我们学过小数除法,所以我就想到把分数除法转化成小数除法计算,将4/5转化成0.8,用0.8除以二等于0.40.4就等于2/5。
我也用了转化的方法,利用商不变的性质,将4/5和二同时乘五转化成四除以十,结果是0.4,也是2/5。
能够想到把分数除法转化成小数除法来解决问题,看来同学们在以往的学习中积累了不少好经验。
请大家观察这三种方法,它们有什么相同之处?
我发现这三种方法都是平均分,都是把五分之四平均分成两份。
我发现他们都是在将计数单位的个数平均分,4/5除以二是把四个1/5平均分成两份,0.8除以二是将三个0.1平均分成两份,而四除以十是将四个一平均分成十份。
他们的发现太有价值了,让我们一起来看看是不是这样。
虽然这些数的组成不同,但是除法的意义和计算的道理都是相通的。
还有其他验证方法吗?
我也用了数形结合的方法来验证,但是我画的图和刚才的不太一样,大家看,把五分之四平均分成两份,每份就是4/5的1/2,也就是说4/5除以二等于4/5乘1/2等于4/10等于2/5。
我发现原来可以把分数除法转化成分数乘法来计算。
画图方法的小改变让你发现了新大陆,真了不起,其他同学你们发现了吗?
听了他的回答,我恍然大悟,从图中我也看明白了,把五分之四平均分成两份,每份就是4/5的1/2,也就是4/5乘1/2。
同学们真是太棒了,想出了这么多方法,经过大家的验证,我们得到结论,4/5除以二等于2/5,每份是这张纸的2/5。
同学们开动脑筋,想出了这么多验证4/5除以二等于2/5的方法,你们真了不起。
如果把长方形纸的五分之四平均分成三份,每份又是这张纸的几分之几呢?
说一说这个问题怎样解决,为什么?
这道题就是把五分之四平均分成三份,求每份是多少?所以用4/5除以三。
有了刚才的经验,请大家自己试着解决这个问题。
时间到了,下面请同学们说一说你的想法。
我想转化成小数进行计算,0.8除以三除不尽,这种方法在这里也行不通,于是我就把4/5和三同时乘五转化成四除以15,最后结果是4/15。
还有其他的方法吗?
开始我还想用把四个1/5直接分成三份的方法,但是我发现这个分数的分子,也就是分数单位的个数,不是三的倍数,我就做不下去了。
小韩,我来帮助你,我也想用把四个1/5平均分成三份方法。
发现被除数的分子不是三的倍数,我就算利用分数的基本性质。
把分数的分子和分母同时扩大三倍,这样被除数就变成了12/15,然后再把12/15平均分成三份,求其中的一份就用12/15除以三等于4/15。
小量的方法太巧妙了,想到了运用分数的基本性质,在分数大小不变的情况下,将分数单位变小,让分数单位的个数变多,然后再把分数单位的个数平均分。
哪位同学还有不同的方法?
我把分数除法转化成分数乘法来计算了,我还画了一幅图,大家看,4/5除以三,表示把五分之四平均分成三份,每份就是4/5的1/3,也就是4/5乘1/3等于4/15,所以每份是这张纸的4/15。
观察这两种方法,你们有什么发现吗?
我发现这两种计算过程都可以用同一幅图表示,只不过第一种方法,先把一张纸平均分成15份,表示出其中的12份,也就是12/15,然后再把12/15平均分成三份,每份就是4/15。
第二种方法是先表示出4/5,再画出4/5的1/3,就是4/15。
通过琪琪的图,我发现它们计算方法虽然不同,但是背后的道理是相同的。由于4/5的分数单位的个数不能平均分,就需要增加分数单位的个数,这就使这个分数的大小不变,分数单位就要变小,和原来的1/5变成1/15,分数单位的个数由原来的四个变成了12个,12个1/15就能平均分了。
第二种方法,我们也可以写成这种形式。
这种形式就和第一种方法是完全相同的,三和三直接约分了,我们就可以直接用分母相同的积做分母,分子相乘的积做分子。
同学们的发言太精彩了,思考也越来越有深度了。我们发现,原来这两种方法之间有着非常密切的联系。
经历了前面的研究,大家有什么想说的吗?
被除数的分子是除数的倍数时,用被除数的分子,也就是分数单位的个数除以除数的方法最简单。
我觉得把分数除法转化成小数除法计算有局限性,因为有些被除数化成小数,结果不能除尽,而转化成整数,有点麻烦。如果数比较大,计算起来不够简便。
经过比较,我发现,其实将分数除法转化成分数乘法的计算方法使用范围最广。
经历了两个问题的研究,同学们对分数除以整数的计算方法理解的越来越透彻了。
分数除以整数,就用分数乘这个数的倒数。
请大家试着计算这两道题。
时间到了,没做完的同学也不要着急,让我们来看看这几位同学是怎样做的,你同意他们的做法吗?
我用的方法是,9/10除以三等于9/10乘1/3等于3/10。
对这种方法你有什么补充吗?
我们一定要注意,计算结果要约分成最简分数。
我们还可以边约分边计算,这样更简便。
这两位同学的提示太有价值了,大家一定要注意。
小兵在计算第二题时,用3/8除以二等于3/8乘1/2等于3/16。
屏幕前的同学们,你们做对了吗?
现在大家能总结一下分数除以整数的计算方法吗?
分数除以整数,如果分子是除数的倍数,那么就用分子除以除数的商作为分子,分母不变,如果分子不是除数的倍数,那么就转化为求这个数的几分之一来计算。
分数除以整数,就用分数乘这个整数的倒数就可以了,所以结果一定要化成最简分数。
把一个数平均分成几份,就是求这个数的几分之一是多少,也就是说都可以转化成分数乘法来计算。同学们赶快大声读一读,看看你是不是也掌握了这些方法。
下面就让我们应用这些方法来计算下面各题。
小芳的第一题是这样写的。
这是小兵计算第二题的过程。
屏幕前的同学们,你们做对了吗?
我特别欣赏同学们在计算过程中注意到能约分的先约分,这样做使得计算更加简便了。
请大家独立完成这道题。
月月想说说自己的解题过程。
通过读题,我知道把妈妈的工作量平均分成三份,小明是这样的,一份,也就是求7/10的1/3是多少?
所以计算小明的工作量就用7/10除以三等于7/10乘1/3等于7/30。答,小明每分钟录入这份文档的7/30。
回答问题真完整,不仅说出了解答过程,还清楚的说出了为什么这样做。
回顾本节课的学习,你有哪些收获?
在这节课中,我知道了小数除法、整数除法和分数除法都有着密切的联系,它们的意义都是相同的,计算的道理也是相同的。
在这节课的学习中,我感受到画图能直观的帮助我们理清思路,解决问题,数学结合真是一种很好的数学学习方法。
我觉得找到新旧知识的联系,巧妙的将新问题转化成旧知识,很多新问题都能迎刃而解。
看来大家不仅学到了新知识,在学习方法上也有不少的收获,相信今天这节课为大家积累了很多数学学习的经验。
这是同学们在刚上课时提出的问题,让我们来看看在这节课中我们找到了哪些问题的答案。
随着大家对分数除法的继续学习,对这些问题也会有越来越深入的认识。
同学们,今天我们学习了分数除法第一课时,具体内容在数学书的第29页。
今天的课后练习是完成数学书第33页第二题和第33页第三题。
这节课我们就上到这里。