数学是一门逻辑性较强的学科，其目标是着力培养学生的观察、分析、推理、综合和解决问题的能力。这就要求数学教师务必要驾驭教材，深入了解、研究教材，深挖教材的内涵，不断拓展思维，培养学生的创造性思维能力。

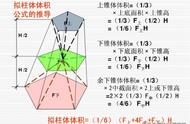
圆柱体积计算公式的推导教学是现行小学六年级人教版数学教材第25页例5之课例。说实在话，从教37年来，虽然我任教小学六年级数学达35年之久，而真正理解教学例题的内涵，深度解剖，直到2015年才悟出其中的玄机。同行们应该都知道该例题图示中，将一个圆柱的底面积分成许多个相等的扇形，能拼成一个近似的长方体，而且所拼成的这个近似的长方体右侧的长方形涂上了红颜色。多年的教学让我突然产生了“灵感”，让我开始思考教材的编者为什么要将其涂上红色呢?原来教材的目的不仅要求教师教会学生圆柱体积的计算公式，而且要更深入了解其内涵，深度解剖，更好地去拓展学生的思维，培养学生思维的广阔性，同时也渗透了两者表面积之间的微妙的变化。下面，我就关于圆柱体积计算公式的推导教学，谈谈我的几点体会：

面向全体夯实基础

掌握和理解圆柱体积计算公式是本节课的重点，也就是说这个要求是针对全体学生的。通过分、拼、观这三个教学过程，先让学生知道了圆柱的体积就等于近似的长方体的体积，进而又得知长方体的底面积正好等于圆柱的底面积，高也正好等于圆柱的高。最后得出“圆柱体积=底面积X高”，即：(V=Sh(V=πr2h)。这样，学生轻松地掌握并理解了圆柱的体积计算公式，教材的基本目标得到了夯实。

培养思维的广阔性

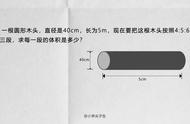
在学生已掌握圆柱体积计算的基础上，我又引导学生仔细观察近似的长方体右侧那个涂红颜色的长方形，并要求他们以红色部分的长方形为底面积时，去求其体积。于是，我设计了这样一道习题：一个圆柱底面半径为1cm，高3cm，其体积是多少?(用两种方法解答)。同学们都很快用前面已学的体积计算公式解答出来了。(即3.14×12×3=9.42cm3)。然而，要用第二种方法解答似乎无从下手，我先给他们一个必要的提示，然后让他们分组讨论5分钟，课堂先是异常的宁静，接着便哗然了……。终于有些学生发现了右边的涂红颜色的长方形的长相当于原来的圆柱的高3cm，宽相当于半径1cm，则底面积是3×1=3cm2。只要用底面积3cm2乘以涂红色部分为底时的高就是其体积了。学生很快便发现了这时的高正好是圆柱体底面周长的一半(即πr=3.14×1=3.14cm)。进而得出其体积的第二种解法为3×1×3.14×1=3×3.14=9.42cm2。这样既拓展了思维，培养了思维的广阔性，也又一次证明了圆柱体积公式的正确性。

深度“解剖”提升学习情趣

为了更好地提升课堂氛围，我又设计了这样一道习题：一个圆柱的底面半径是3cm，高是4cm，若将其底面分成许多个相等的扇形，剪开后拼成一个近似的长方体。圆柱体与所拼成的近似的长方体的表面积谁大?顿时，课堂沸腾了，有的说因为这个长方体是圆柱体拼成的，它表面积相等;有的说长方体的表面积比圆柱体多了一个红色的长方形;还有的说长方体的表面积比原来的圆柱的表面积多了两个长方形……。通过讨论，空间想象，解剖图形，同学们都理解了第三种说法是正确的。其实右边涂红色部分的那个长方形和它所相对的相等的长方形的面积之和就是比原来的圆柱体所增加的面积。并且，每个长方形的长就是原来的圆柱的高，宽就是原来圆柱的底面半径。所以近似的长方体的表面积比圆柱表面积多的面积就是2个长方形的面积(即：4×3×2=24cm2)。

由于教学中，我深入研究了教材，深度解剖分析，积极引导学生观察、分析、推理、综合、解答，让学生对圆柱体产生了极大的情趣。从表象到解剖，从一般到特殊、从平到坡、从基础到拓展、创造·……。极大地调动了学生学习的主动性、积极性，全方位提升了课堂教学的效果。

作者:康王乡中心小学 周述华 张世宏