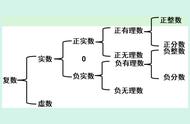
自然数是正整数的集合,通常用符号N表示,即N={1, 2, 3, 4, 5, ...}。自然数是最基本的数学概念之一,它们通常用于计数和度量。自然数包括所有的正整数,但不包括0和负整数。例如,自然数中的第一个数是1,第二个数是2,第三个数是3,以此类推。自然数在数学中有着广泛的应用,例如在代数、几何、数论、概率论和统计学等领域中。
二、谁发明了自然数,为何发明自然数自然数并不是人类发明的,而是一种数学上的基本概念,是描述自然界中事物数量的数学工具。
自然数最早是由人类用于计数的。古代人类用自然数来计算他们所拥有的财产、农作物和家畜的数量等。自然数的概念随着人类社会的发展而逐渐形成,但并没有一个具体的人发明自然数的概念。在古代文明中,如古希腊、古印度和古中国,人们都有自己的数学体系和记数方法,但都有类似自然数的概念。
在现代数学中,自然数是一个基本的数学概念,它被广泛地应用于各个数学领域。自然数是数学研究中的基础,是其他数学对象的基础。例如,在代数学中,自然数是整数、有理数和实数的基础;在数论中,自然数是研究素数、质因数分解和算术函数的基础;在几何学中,自然数是描述空间和形状的基础。
三、有哪些神奇的自然数自然数中有很多有趣和神奇的性质和特征,以下是其中一些:
- 37是一个神奇的自然数,因为如果你写下任何数字(不是0),然后按顺序颠倒数字并将它们相减,最终的结果总是37。
- 自然数中最小的质数是2,它是唯一的偶质数,其他所有偶数都不是质数。
- 黄金比例(Golden Ratio)是一个特殊的数,它约等于1.6180339887...,在数学、艺术和自然界中都有广泛的应用。黄金比例的定义是:将一个线段分成两段,使其中一段与整个线段的比等于另一段与这一段的比。
- 自然数中有无穷多个素数,素数是只能被1和它本身整除的正整数,例如2、3、5、7、11等。这个定理被称为欧拉素数定理(Euler's Prime Number Theorem)。
- 自然数中最大的素数目前已经超过了400万位数字,这是由一些计算机组成的志愿者网络使用分布式计算方法进行的,这个素数被称为Mersenne素数。
- 自然数中存在一些完全数,这些数的所有真因子(除了自身以外的因子)之和等于该数本身。例如,6是一个完全数,因为6的真因子是1、2、3,它们的和正好等于6。
- 斐波那契数列(Fibonacci Sequence)是一个经典的数列,每个数都是前两个数的和,该数列的前几个数字是1、1、2、3、5、8、13、21、34、55等。这个数列在自然界中广泛出现,如植物的叶子排列、贝壳的螺旋排列、动物体型比例等。