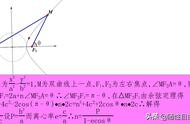
古文明是现代科学的启蒙,是理性思维的源泉,而天文学与几何学是古希腊文明的主导与核心,球面和圆锥截线的认识是古文明中几何学的至高点反比例函数的图象称为双曲线,用折纸或截面的操作方法可得到双曲线。如图,准备一张圆形纸片,并在圆外取一点F,然后折叠纸片,使F点落在大圆的圆周上,这样不断地折下去,这一系列折痕就构成了双曲线的一个分支。

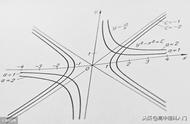
如图,用平面去截一个双头圆锥,圆锥和平面相交所得的曲线有圆、椭圆、抛物线、双曲线。椭圆、抛物线、双曲线统称为圆锥曲线,公元前200多年,古希腊人阿波罗尼斯就发现了这一现象。

双曲线既是轴对称图形,又是中心对称图形。正则圆,歪则椭,点点繁星,皎皎星光,发人深思,令人神游,而太阳系永恒之舞的基本节奏与舞步却是圆锥曲线。
公元1896年,挪威生理学家古德贝尔对闭眼打转的问题进行了深入的研究。他收集了大量事例后分析说:这一切都是由于人自身两条腿在作怪!长年累月养成的习惯,使每个人一只脚伸出的步子,要比另一只脚伸出的步子长一段微不足道的距离。而正是这一段很小的步差x,导致了这个人走出一个半径为y的大圈子!
现在我们来研究一下x与y之间的函数关系:
假定某个两脚踏线间相隔为d。很明显,当人在打圈子时,两只脚实际上走出了两个半径相差为d的同心圆。设该人平均步长为l。那么,一方而这个人外脚比内脚多走路程2π(y d/2)-2π(y-d/2)=2πd:另一方面,这段路程又等于这个人走一圈的步数与步差的乘积,即:2πd=(2πy/2y)x,化简得y=2dl/x。
对一般的人,d=0.1米,1=0。7米,代入得(单位米)y=0.14/y,这就是所求的迷路人打圈子的半径公式。今设迷路人两脚差为0。1毫米,仅此微小的差异,就足以使他在大约三公里的范围内绕圈子!
上述公式中变量x,y之间的关系,在数学上称为反比例函数关系。所谓反比例函数,就是形如y=k/x(k为常量)这样的函数。它的图象是两条弯曲的曲线,数学上称为等边双x曲线,在工业、国防、科技等领域都很有用场。

一、有关面积关系:
1.反比例函数图像上任取一点A,然后过A点分别向x轴,y轴作垂线,垂足分别为为B、C,则矩形ABOC的面积始终等于k的绝对值。