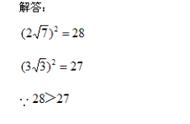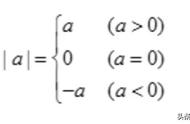有理数比较大小需要根据所给的数据灵活变通，选择正确的方法会起到事半功倍的效果，方法选择错误，可能会做对，但是花费的时间相对较多。有理数比较大小的方法，除了作差法外，你还知道哪些呢？

可以利用数轴比较大小，数轴上，越往右越大，越往左越小。有些题目需要结合绝对值和相反数的概念，互为相反数的两个数在原点的两侧，到原点的距离相等。

例题1：已知a＞0，b＜0，且|a|＜|b|，试比较a、-a、b、-b的大小．

分析：由于a＞0，b＜0，则a在原点的右边，b在原点的左边，又|a|＜|b|，知a离原点的距离小于b离原点的距离，在数轴上表示出a，b，再根据一对相反数在数轴上的位置特点：分别在原点的左右两边，并且离开原点的距离相等，在数轴上又可以表示出-a，-b，最后根据在数轴上表示的数，它们从左往右的顺序，就是它们由小到大的顺序，从而得出结果．

有些小题无法直接比较大小，可以利用特殊值比较大小。比如例题1，可以假设a=2，b=-1，那么-a=-a，-b=1，由于-2＜-1＜0＜1＜2，那么-a＜b＜0＜-b＜a。

例题2：已知a＞1，b＞1，且a＞b，试比较a 1/a与b 1/b的大小．

分析：由题意可设a=3，b=2，那么a 1/a=10/3，b 1/b=5/2，那么a 1/a＞b 1/b。

作商比较法是比较两个数大小的常用方法，当比较的两个正分数作商易约分时，作商比较往往能起到事半功倍的效果；当这两个数是负数时，可先分别求出它们的绝对值，再作商比较它们绝对值的大小，最后根据绝对值大的反而小下结论。