[思路导航] 问题分析,要证线段相等,掌用的方法有:
证明角相等,三角形中等角对等边
证明所在的两个三角形全等
证明是线段垂直平分线上的点
三角函数值法
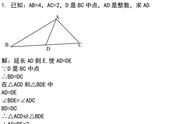
将已知标示如下:

方法一、先从30°三角形入手、构造直角三角形利用相关条件证明
证明:如图,作CP⊥AD,DQ⊥BC,垂足分别为P、Q

∵AC=AD
∴∠ACD=(180°-30°)/2=75°
又∵在Rt△PCA中∠CAP=30°
∴∠ACP=60°
∴∠PCD=75°-60° =15°
∵∠ACB=90°
∴∠BCD=90°-75°=15°
在Rt△PCD与Rt△QCD中
∠CPD=∠CQD
∠PCD=∠QCD
CD=CD
∴Rt△PCD≌Rt△QCD(AAS)
∴CQ=PC
∵∠CAD=30°
∴PC=AC/2
又∵AC=BC
∴CQ=BC/2
∴DQ是BC的垂直平分线
∴CD=BD
小结:此方法为从已知出发,根据等腰、直角、30°等条件构造特殊三角形。
方法二:结合题目中AC⊥BC,30°角,利用矩形知识,直接考虑证明D是线段BC垂直平分线上的点
证明:如图,过D作DN⊥BC,AM⊥AC,AM与ND延长线交于M