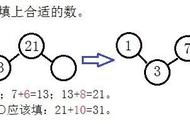
前面两期，我们讲了怎样用多种方法，来做鸡兔同笼的基础题和一种变形。

分别是：

由易到难列表法

灵机一动假设法

公平交换代换法

一目了然图形法

（前两期看这里:

）

那么，如果在题目上再加点变化，你还能不能做了：

鸡兔同笼，共有脚100只，如果将鸡换成兔，将兔换成鸡，则共有脚86只。问：鸡、兔各有几只？

方法一：列表法

首先，还是从极端的情况开始列表。如果笼中动物全部是鸡，因为脚有100只，所以鸡的数量为50只。鸡兔交换后，变成50只兔子，脚的数量为200只。

然后，逐步减少鸡的数量，增加兔子的数量，要注意交换前鸡兔的脚数之和要始终等于100.

列出前面若干项后，很容易找出数量变化的规律，再解题就很容易了。

方法二：假设法

我们把交换前的鸡兔叫做第1笼，交换后的叫做第2笼。

如果把第1笼和第2笼关在一起，那么笼中的鸡和兔正好一样多了。把一鸡一兔看做“一对”，每一对有6只脚，共有100 86=186只脚，可算出共有186÷6=31对。

这样，就得到了一个基础的鸡兔同笼问题了：鸡兔共有31只，共有脚100只。

这道题还可以这样假设：如果在交换前再放入7只鸡，那么交换后，总的脚数会不变。所以交换前，兔子比鸡多7只。这样，我们又把问题转化成了第二辑中做过的鸡兔同笼变形题了。

方法三：代换法

在用代换法解本题时，会用到等式的另外一个性质：等式两边同时乘以一个相同的数（0除外），等式仍然成立。

那么，利用上述性质，消去其中的一个符号，就可以解题了。

本题还可以用图形法来做，但用图形法的话，不够简洁、直接，失去了图形法自带的不言自明的优势，所以就不在此介绍了。

再回过头来看上面三种解法。

列表法的重要性一直被低估了，它其实是一种归纳法。

做鸡兔同笼问题的一般是年纪比较小的学生。这个年龄段的孩子，还很难通过抽象思考，理解和发现本题中数量之间的关系。所以，往往题目稍微一变，就不会做了。列表法对他们来说是一种很实用的方法，也能用来辅助抽象分析和思考。

假设法可以鼓励学生大胆的想象，发挥创造力，尝试多种解题的可能。如果可以提出一些又有趣又巧妙的假设，对于提高学生学习的兴趣也很有帮助，把数学当成游戏，把解题玩起来。

而代换法可以为学习方程做准备，包括熟悉的符号的使用，理解等式的性质，还可以逐渐习惯怎样用抽象符号进行计算。

我们的轻数学课也做了一个鸡兔同笼的模块课，春节前上线了，课堂效果挺好，孩子们学到了方法，课上的也挺开心。如果家长们感兴趣的话，请联系小概率先生，*mrxiaogailv