板块模型即是“滑块—滑(木)板”模型 。一般涉及长木板和滑块,且二者产生相对运动。隔离法分析二者受力情况,确定物体的运动情况的基础 。伴随着临界问题和多过程问题,使此类问题变得较为复杂。
特点:上、下叠放,且两物体在摩擦力下发生相对运动。上下两物体共速时,摩擦力可能突变,因此合外力可能突变,两者加速度可能突变。两物体运动形式发生变化因此而产生临界问题和多过程问题

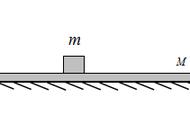
水平面上的常见四种情形
动力 学观点 | 分别对滑块和滑板进行受力分析,根据牛顿第二定律求出各自的加速度;从放上滑块到两者速度相等,滑块和滑板运动的时间相等,由v共=v0-a1t=a2t可求出共同速度和所用时间t,然后由位移与时间的关系可分别求出两者的位移。以及两者之间的相对位移(画出运动示意图更形象更直观)理解相对位移的含义。可以用相对运动知识来帮助理解 具体思路: 1.板块模型可以千变万化,掌握好“三图”则一切可解(运动示意图,受力分析图,v-t) 2.判断滑块是否掉下来的方法不同: ①②是达到共速时,相对位移是否大于板长 ③④系统初速度为0,在木板或滑块施加水平力F。是判断能否保持加速度一致 3.当板与块速度相等时,应注意判断接下来能否相对静止 |
单独对图中四种情况,临界条件的判断比较和讨论

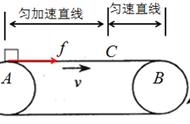
图一
图1滑块具有初速度,v0滑上长木板。分析小滑块的受力,受到重力支持力和向左的滑动摩擦力。小滑块以初速v0向右做匀减速运动。分析长木板的受力,与地面光滑,因此在水平方向上,长木板受到向右的滑动摩擦力。所以长木板应该是向右做匀加速直线运动。
所以长木板做匀加速直线运动小滑块匀减速直线运动中间应该会有一个共速的条件。画出两者的vt图像。因此可以计算出两者共速的速度大小,以及达到共速所用的时间。进而计算出两者共速的位移以及相对位移。
讨论有两种情况第一种情况就是相对位移大于板长说明公诉之前就已经从长木板的右侧掉下来了。相对位移小于板长,以后应该以相同的速度匀速直线运动。

图二
图二而言,分析情况和图一类似。不过此时了,小滑块呢是匀加速直线运动,长木板是以初速v0向右做匀减速直线运动。受力分析,求出两者的加速度。画出长木板和小滑块的vt图像。进一步计算出两者共速的速度大小,以及所用时间。进一步算出小滑块和长木板,共速的位移。以及两者的相对位移。讨论相对位移与板长的大小关系。进入不讨论,两者能否相同的速度以然后匀速运动。

图三
由于图三的小滑块水平向右的拉力作用。把小滑块和长木板看成整体,也受到一个水平向右的拉力作用。
先讨论第一种临界条件。当拉力f比较小的时候,系统以相同的加速度向右匀加速运动。长木板和小滑块的加速度相同。长木板做加速运动提供的外力由小滑块的摩擦力提供。条件就是两者之间为滑动摩擦力瞬间。这样可以求出临界的加速度a=μg以及临界的拉力。
当f继续增大。两者之间发生相对滑动。长木板而言受到水平向右的滑动摩擦力长木板上向右做匀加速直线运动。对小滑块而言,水平方向受到向右的拉力作用,以及向左的滑动摩擦力作用。也可以算出小滑块的加速度大小。小滑块也向右做匀加速直线运动。
可以讨论两种情况:1.小滑块的加速度大于长木板的加速度。此时拉力f较大。小滑块将从长木板的右侧掉下来。画出vt图像,也可以算出掉下来,所用的时间。
2.小滑块的加速度小于长木板加速度。这种情况小滑块在两者相对运动的瞬间,直接从长木板的左端掉下去。这没有明显的实际应用。

图四
对图四的分析和图三的分析是一样的。第一种临界条件,长木板和小滑块一起向右匀加速。临界点就是两者恰好发生相对运动,小滑块的合外力,向右的滑动摩擦力,恒定因此小滑块向右做匀加速直线运动。长木板的合外力为向右的拉力和向左的滑动摩擦力。两者都是向右做匀加速直线运动,只有当长木板的加速度大于小滑块的加速度,才有实际应用意义。这样最终小滑块将从长木板的左侧滑下。水平拉力的临界条件f=μ(M m)g。可以分别画出两者的vt图像,也可以计算出滑下来所用的时间。大小就是木板的长度。