平面曲线弧长是微积分学中的重要内容,它的推导很简单,黎曼和加上你已有的数学基础就可以理解,今天我们从切线的角度出发来分析下
首先回忆下教材的内容
假定f的图形以(a,c)为起点,以(b,d)为终点,把它表示成如下图的分割区间,以至于在其上的曲线弧近似是直的。

逼近子区间上方的曲线弧的线段的长度是

逼近整个曲线的长度是,

严格的说要用对每个子区间上对于f应用中值定理,就把这个和改写成为黎曼和(伙伴们你理解这句话是要表达什么意思吗?为什么这里会用到中值定理呢?)可以留言讨论
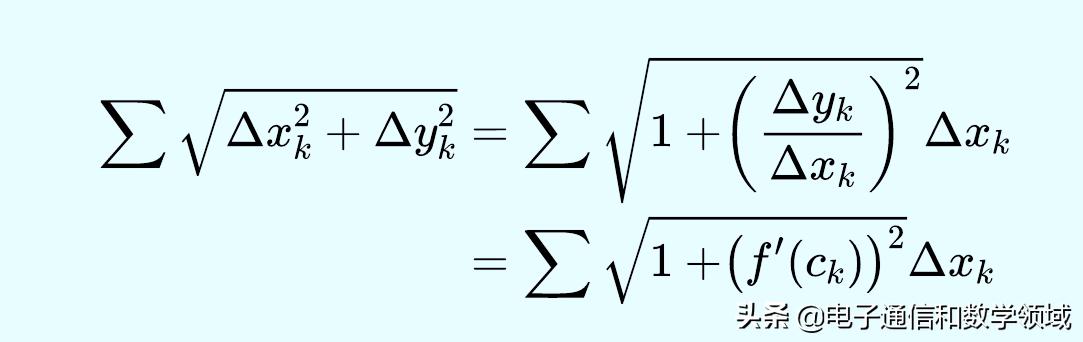
平面曲线弧长是微积分学中的重要内容,它的推导很简单,黎曼和加上你已有的数学基础就可以理解,今天我们从切线的角度出发来分析下
首先回忆下教材的内容
假定f的图形以(a,c)为起点,以(b,d)为终点,把它表示成如下图的分割区间,以至于在其上的曲线弧近似是直的。

逼近子区间上方的曲线弧的线段的长度是

逼近整个曲线的长度是,

严格的说要用对每个子区间上对于f应用中值定理,就把这个和改写成为黎曼和(伙伴们你理解这句话是要表达什么意思吗?为什么这里会用到中值定理呢?)可以留言讨论
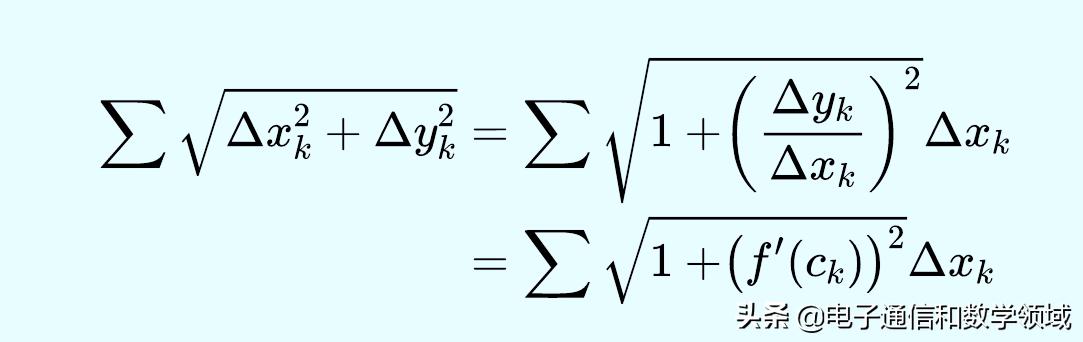











Copyright © 2018 - 2021 m.360kss.com., All Rights Reserved.