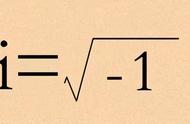其中 x 是任意实数。欧拉公式把指数函数和三角函数联系起来，它在复数学、微积分以及物理学中都有广泛的应用。欧拉公式的证明需要使用复变函数的知识，这里就不深入展开了。但是我们可以通过一个简单的例子来看看欧拉公式的应用。

假设我们需要求解方程 x^2 1=0 的根。我们可以将方程转化为 x^2=-1，进而得到 。因为开根号是一个实数运算，而 并不是实数，所以我们需要利用虚数来表示根。

根据欧拉公式，我们可以将 表示为 。因此，原方程的两个根可以写成 。这就充分展示了欧拉公式的应用价值。下面是欧拉公式的图示解释：从图中可以看出，欧拉公式的实部和虚部分别对应了一个以原点为起点、以 e^(i*θ) 为终点的向量的 x 轴和 y 轴分量。同时，由于 sin 和 cos 都是周期函数，因此该向量将会沿着单位圆旋转，直到回到原点。

虚数在电路分析、信号处理、量子力学、统计力学等领域都有广泛的应用。

在电路分析领域中，复数被用于表示交流电信号的振幅和相位角度。当我们需要处理一条以正弦波为基础、幅值和相位都可变的交流电路时，虚数就能够派上用场了。我们可以通过复数来表示电路中的电压和电流大小和相位的关系。如下I = V0 / Z的简易RLC电路图。

在信号处理领域中，复数被用于傅里叶变换和频谱分析。由于频谱是由一系列正弦波组成的，因此可以用复数表示各个频率上的幅值和相位，从而帮助我们更好地分析和处理信号。

例如：在信号处理领域，复数被广泛地用于傅里叶变换和频谱分析。傅里叶变换是把一个复杂的函数分解成若干个简单的正弦或余弦波的加权组合。这让我们可以更好地理解函数的构成和特点。下图展示了一个简单的函数 $f(x) = 2\sin(2\pi x) 3\sin(4\pi x)$ 和它的傅里叶变换。

我们可以看到，这个函数经过傅里叶变换后，被分解成了两个不同频率的正弦波的加权组合。这些正弦波对应着原始函数中的不同特征，它们的振幅和相位差反映了函数的构成和性质。

在物理学领域中，虚数被用于描述粒子的波动性。例如，在波动光学中，我们可以利用复数表示电场和磁场的振幅和相位关系，从而描述光的传播特性。下图显示了一束经过狭缝后的单色光的衍射图案，这种衍射现象只能通过复数来描述。