物理学上把本身的线度比相互之间的距离小得多的带电体叫做点电荷。相当于运动学的“质点”模型。在定量地研究电荷之间相互作用的时候，发现有些电荷的大小对所研究问题的结果带来的影响微不足道，这个时候就完全可以把电荷的体积和大小忽略掉，把电荷看做只有电量，没有大小的电荷，这就是点电荷模型。实际中，电荷均匀分布的孤立导体球，就外部电场而言，与电量集中在球心的点电荷所形成的电场，形式上没有丝毫差异。

一、两点电荷的库仑力

F=kQq/r²

和万有引力F=GMm/r²类似。

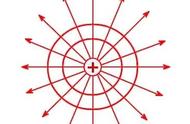
二、点电荷激发电场的场强

E=kQ/r²

和引力加速度a=GM/r²类似。

三、两电荷的电势能

Ep=kQq/r（取无穷远为零电势能点）

和引力势能Ep=GMm/r²类似。

四、点电荷激发电场的电势

φ=KQ/r(取无穷远为零电势点）

是由场源电荷Q和距离r决定。

和引力势Ψ=GM/r类似。

半径为R的导体球面的电势，应当等于电量集中在球心的点电荷，在R处的电势，即KQ/R。根据静电平衡，整个球体内部和表面的电势都相等，是同一数值。而球体外部电势的大小，则与到球心的距离成反比。