卡诺将热机做功的过程总结成包括两个等温过程和两个绝热过程的卡诺循环，即提出了由绝热膨胀、等温压缩、绝热压缩和等温膨胀4个步骤构成的“理想热机”。卡诺第一个指出，热机必须工作于两个不同的温度之间，热机的效率是两个温度差别的函数。卡诺定理认为，“所有工作在同温热源与同温冷源之间的热机，可逆热机的效率最高”。卡诺定理实质上可以看作是热力学第二定律的理论来源。

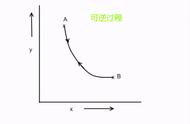
一个物体的边界如果没有任何形式的传热方式，则被定义为绝热，是保温与保冷的统称。

某一物质系统经过某一过程，由某一状态变到另一状态，如果存在另一过程，它能使物质系统和环境完全复原，即物质复原到原来状态，同时消除了原来过程对环境所产生的影响，则原来的过程称为可逆过程。

卡诺热机包含了可逆过程。可逆过程发生的很慢，因此这个过程可以被看作是一平衡态，整个过程是可逆的，并且其中没有热交换和工作量的变化。例如，一个气体存储在一个有着紧密贴合内壁，可移动，无摩擦的活塞的气缸内，并可以通过一个可逆过程等温压缩，只要被压缩的非常慢。不是所有非常慢的过程都是可逆的，如果存在摩擦，比如刚刚所说的汽缸和可移动活塞之间，过程单向的被完成（从状态A到B）不会是状态B到A的逆状态。这种过程不会被认为是可逆的。当然一个完美的可逆过程在现实中是不可能的，因为这个需要无限的时间；可逆过程可无限被接近，这是一个非常重要的理论。

所有现实中的过程都是不可逆的：他们做不到绝对慢。气体中会出现紊流，摩擦力会出现等等；任何过程都不能准确的在可逆过程中完成，因为因摩擦产生的热不会逆转成它自己，紊流会不一样等等。给定体积的气体不会有一个确定的压力P和温度T，因为系统不会一直处于一个平衡态。因此一个真实，不可逆的过程不能被呈现在PV图像上，除非它接近理想过程。但是一个可逆过程总是可以呈现在PV图像上；一个可逆过程，当可逆的完成时，原路按PV图像上返回。虽然所有真实过程都是不可逆的，可逆过程在概念上非常重要，就像理想气体那样。

只有当系统的状态变化过程进行的无限缓慢，在进行过程中没有能量损耗的准静态过程才是可逆过程，否则就是不可逆过程。

可逆过程是一个可以往反方向进行而使系统和外界环境复原的过程。

可逆过程一定是无摩擦的准静态过程（摩擦会引起热功转换）。

反之，如果用任何方法都不可能使系统和环境完全复原，则原来的过程称为不可逆过程。

3.1 可逆过程的特点

3.1.1 可逆过程是以无限小的变化进行的（推动力无限小），系统内部及系统和环境间都无限接近平衡，进行得无限慢。

3.1.2 过程结束后，系统沿着原途径逆向进行恢复到始态，环境也同时复原，无任何耗散效应。

3.1.3 在等温可逆膨胀过程中系统对环境做最大功，在等温可逆压缩过程中环境对系统做最小功。

3.2 不可逆过程的特点

3.2.1 自然界中一切自发过程都是不可逆过程；

3.2.2 不平衡和耗散等因素的存在，是导致过程不可逆的原因，只有当过程中的每一步，系统都无限接近平衡态，而且没有摩擦等耗散因素时，过程才是可逆的；

3.3 不可逆过程并不是不能在反方向进行的过程，而是当逆过程完成后，对外界的影响不能消除。

可逆与不可逆是标志自然过程方向性的物理概念。某一物质系统经过某一过程，由某一状态变到另一状态，如果存在另一过程，它能使物质系统和环境完全复原，即物质复原到原来状态，同时消除了原来过程对环境所产生的影响，则原来的过程称为可逆过程。反之，如果用任何方法都不可能使系统和环境完全复原，则原来的过程称为不可逆过程。在经典力学和量子力学中，牛顿运动方程和薛定谔方程表现的是可逆性。即它们都包含有时间，但不包含时间的箭头，时间仅仅是运动的一个几何参量，取正或取负都有相同的功能。在热学中，热总是自发地从高温部分传向低温部分，最后达到热平衡状态，描述这类热传导过程的是傅立叶方程，它刻画的是不可逆性。热力学第二定律揭示了过程的单向性，描述了时间的不可逆性。它指出，对于一个孤立系统中的不可逆过程，熵会随着时间的流逝而增大，从而把演化的概念引进了物理学。现代自然科学越来越多地揭示了自然界发展的方向性和时间的不可逆性，如天体的演化，地壳的变迁，生物的进化等等。

严格的物理学意义上的可逆性是指时间反演，即过程按相反的顺序进行。在经典力学的运动方程中，把时间参量 t 换成 -t，就意味着过程按相反的顺序历经原来的一切状态，最后回到初始状态。但实际上，机械运动过程总是受到各种复杂的随机因素的作用，因此完全的可逆性是不存在的。

严格的物理学意义上的不可逆性概念最初是由经典热力学提出的。它把热的过程区分为可逆的和不可逆的两种，并指出在一个封闭系统的热过程中，热量总是自发地从较热物体传输给较冷物体。热力学第二定律用熵的增加来描述这种不可逆过程。这个定律的统计解释表明，不可逆过程就是封闭的分子系统从有序状态趋向于无序状态，一切自然过程总是沿着分子热运动的无序性增大的方向进行。

热力学第二定律的每一种表述，都揭示了大量分子参与的宏观过程的方向性，使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性。

化学及热力学中所指的熵（Entropy），是表示分子状态混乱程度的物理量。是一种测量在动力学方面不能做功的能量（“无法利用的能量”）总数，也就是当总体的熵增加，其做功能力也下降，熵的量度正是能量退化的指标。熵亦被用于计算一个系统中的失序现象，也就是计算该系统混乱的程度。熵是一个描述系统状态的函数，但是经常用熵的参考值和变化量进行分析比较，它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。

1865年，克劳休斯将发现的新的状态函数命名为，用增量定义为

式中T为物质的热力学温度；dQ为熵增过程中加入物质的热量，下标“r”是英文单词“reversible‘’的缩写，表示加热过程所引起的变化过程是可逆的。

若过程是不可逆的，则

下标“ir”是英文单词“ireversible‘’的缩写，表示表示加热过程所引起的变化过程是不可逆的。

合并以上两式可得