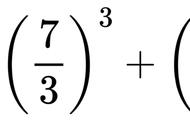这其实就是一个P/NP问题——是否有一种方法，让集卡的过程轻而易举？

所以，GPT-4是怎样得出P≠NP的？让我们往下看。

97轮对话，给出P≠NP结论

在这项研究中，研究者GPT-4学会了一种「苏格拉底式推理」。

他们引入了五个不同的角色（比如精通概率论的数学家），作为协助证明者，根据自己擅长证明不同的部分。

GPT-4用这种方法，开发了一种推理路径，得出了和北航Ke Xu、北工商Guangyan Zhou（论文三作和四作）最近提出结果一致的结论！

论文地址：https://arxiv.org/pdf/2302.09512.pdf

在最初的14轮对话中，GPT-4被引导设计出了初步的证明模式。

GPT-4被问的第一个问题是：「你能从哲学角度而不是计算机理论角度找到P!=NP问题背后的根本问题吗？」

在这个提示中，技巧在于鼓励模型创造性回答，避免进行检索。比如，「如何证明 P!=NP」这样的提示可能会引导大模型进行检索。

用上「苏格拉底式推理」中的转换模式后，就可以生成更具创新性的回答。

对于这个问题，GPT-4是这么回答的——

P!=NP问题背后的基本哲学问题，可以看作是创造力、直觉和洞察力（通常与NP问题相关）与系统化、算法和确定性方法（与P问题相关）之间的矛盾。

如果P=NP，那就意味着宇宙有一种基本的简单性，表面上看似复杂的问题都有高效、优雅的解决方案。