图解：非线性路径的各个边上的切线。

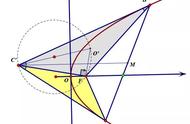
顾名思义，切向速度描述了物体沿圆周的运动，该物体在圆周上任一点的方向始终与圆周相切。但该概念不仅限于匀速圆周运动，也适用于所有非线性运动。如果物体通过非线性曲线从点A移到点B，则红色箭头表示该轨迹上各个点的切向速度。

我们继续研究这个圆。

切向速度公式

首先计算角位移q，它是物体在圆周运动时的圆弧轨迹s的长度与半径r的比值，即圆弧投影下位于从中心开始并连接到其两端的两条线之间的角部分，单位是弧度。

角速度就是物体角位移的变化率，用ω表示，其标准单位为弧度/秒(rad/s)。与线速度不同，它只适用于圆周运动，本质上是角位移扫掠的速率。

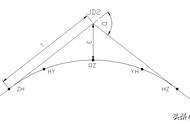
图解：匀速圆周运动中线速度或切向速度的推导。

角速度的线性分量就是线速度，即物体线性位移的变化率。线性位移是上面提到的的圆弧轨迹的长度，半径r和角位移q乘积的导数就是物体的线速度。半径是常数，不包括在运算中；物体的线速度就是角速度和圆弧轨迹半径的乘积。

圆周运动的物体，在任意时刻的线速度，等于它的切向速度！

线速度还可以用周期来定义。如果把物体绕圆旋转一次所需的时间定义为周期，则其圆周运动的速度为s / t（距离/时间）。

图解：线速度或切向速度v与周期 T之间的关系推导。

T的倒数叫作频率，是每秒包含的周期数，用f表示。 2pf的乘积称为角频率，用w表示，这有助于我们得出先前的结果。

矢量积

注意切向速度是矢量，既有大小也有方向。标准符号上方的箭头表示矢量。切向速度的方向即使在不断变化，矢量积也是不变的。所有矢量都可以写成两个矢量的矢量积，也就是两个矢量的长度大小和它们之间夹角正弦的乘积，矢量积的方向和原先两矢量垂直。

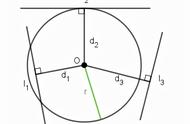
图解 :为什么切向速度的值不随方向的变化而变化呢？也就是说，任一点的切向速度，数值相同但方向不同。

我们需要算矢量积的是半径r和角速度ω。根据右手定则，如果用右手握住旋转轴并沿物体的旋转方向旋转手指，则拇指指向角速度方向，很明显角速度和半径垂直。并且由于90度角的正弦值为1，因此在圆周上任意点得到的两者矢量积将始终保持不变。

有趣的是，物体在圆周内和圆周上具有相同的角速度，但切向速度不同。如其公式所示。这是因为半径的差异。因此，从旋转木马边飞出的人比从内部飞出的人速度更快，落点更远。