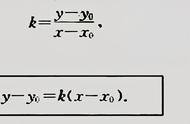建立数学直观是非常重要的。在现代数学教学中，数形结合的教学是建立数学直观的有力工具。由于直角坐标系的发明，使得代数式与图形有机结合，这也是微积分产生的重要基础性工作之一。在直角坐标系下，借助距离公式可以用代数式表达直线，圆，椭圆，双曲线等几何图形，将几何问题代数化。不仅如此，利用直角坐标系的几何直观，还可以解决数据分析等重要问题。

建立直观是非常必要的，就教育而言，直观是一种判断能力，是凭借专业直觉对事物作出直接判断的能力，包括从条件预测结果的能力，也包括由结果探究成因的能力。这种能力依赖于专业知识，但更依赖于经验：依赖于经验的积累，依赖于经验的浓缩，依赖于经验的升华，这些都与我们正在讨论的核心思想“抽象”有关，因为浓缩与升华的基础是抽象。因此，对于任何学科的教学，最终都应当把培养学生的学科直观作为重要的价值取向。在现代数学教学中，数形结合的教学是建立数学直观的有力工具。

至少到16世纪，当人们理解负数和无理数遇到困难时，就想到了用图形来表示数量。虽然还不能给出无理数有说服力的定义，但时意大利数学家庞贝利和荷兰数学家斯蒂芬等都主张在数与数轴之间建立一一对应的关系，还定义了长度的四则运算，并以此解释了实数的四则运算。

上图描绘的就是数轴，是一个有方向和单位长的直线，整数被表示为数轴上一组等距离的点，正整数在0的右边，负整数在0的左边。如果把一个单位长分为n等份，那么，每一个小单位表示了1/n的大小，分数 m/n是由0开始向右数出m个小单位所对应的点。事实上，我们也能在数轴上表述代数数，比如对于√2，可以用边长为1的正方形的对角线的长度在数轴上找到对应的点。

这样，对于给定的数a，用|a|表示对应的点到0点的距离，称之为a的绝对值。因为距离不能小于0，因此，当a≧0时，|a|=a；当a<0时，|a|=-a。

进一步，对于数a和b，不妨设a<b，我们在数轴上找到对应的点，称这两个对应点之间的线段为区间，用[a,b]表示。那么，对应属于这个区间的点c，表示c∈[a,b],必然有a<c和c<b。现在已经把数轴上的点与数有机地对应起来了，很容易验证，无论区间长度多么小的区间内总是有有理数存在，于是我们说在数轴上有理数是稠密的，但是有理数不能覆盖数轴，因为还有√2这样的代数数；很显然，代数数也是稠密的，但是代数数也不能覆盖数轴，因为还有π这样的超越数。借助数轴，我们似乎可以给实数一个直观的描述：能够覆盖数轴的所有数的全体，包括有理数以及有理数以外的实数，称之为无理数，可是应当如何来准确地定义无理数从而定义实数呢？为了做到这一点，人们还需要相当多地准备，还需要相当长的时间。

我们还是先谈图形结合对于数学发展的作用。关于图形结合的根本性工作是由两位法国数学家笛卡尔和费马完成的。柯郎在他的著作《什么是数学》中说，费马的工作是在1626年，笛卡尔的工作是在1637年完成的。他们把数对与平面上的点一一对应起来，从而发明了解析几何，现在解析几何已经成为高中阶段数学课程中很重要的教学内容。解析几何的核心是直角坐标系（也称笛卡尔坐标系），这是由两个相互垂直的数轴构成的，一个方向向右，一个方向向上，分别称为x轴（横坐标）和y轴（纵坐标）；两个O点重合，称之为原点。那么，一个数对(x1,y1)就对应于直角坐标系上的一个点A(x1,y1)，即横坐标为x1，纵坐标为y1的点。现在平面被直角坐标系的两个轴分割成四个部分，我们称为四个象限，两个坐标均为正值的象限被称为第一象限，然后按逆时针方向分别命名为第二，三，四象限。有了这些基础性的工作，就可以用代数的方法来分析几何问题了，现在人们称这样的工作为代数几何。