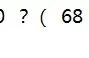第1课时　平移的认识

1．理解并掌握平移的定义及性质；(重点)

2．能够根据平移的性质进行简单的平移作图．

一、情境导入

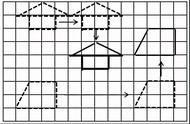
观察下列图片，你能发现图中描绘的运动的共同点吗？

二、合作探究

探究点一：平移的定义

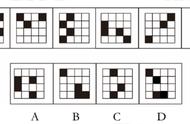
下列各组图形可以通过平移互相得到的是(　　)

A. 　B.

C. 　D.

解析：根据平移不改变图形的形状和大小，将题中所示的图案通过平移后可以得到的图案是C，故选C.

方法总结：本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小．

探究点二：平移的性质

【类型一】 利用平移的性质进行计算

如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1，若BC＝3，△ABC与△A1B1C1重叠部分面积为2，则BB1等于(　　)

A．1 B. C. D．2

解析：设B1C＝2x，根据等腰直角三角形和平移的性质可知，重叠部分为等腰直角三角形，则B1C边上的高为x，∴×x×2x＝2，解得x＝2(舍去负值)，∴B1C＝2，∴BB1＝BC－B1C＝.故选B.

方法总结：本题考查了等腰直角三角形的性质和平移的性质．关键是判断重叠部分图形为等腰直角三角形，利用等腰直角三角形的性质和重叠部分面积列出方程，求重叠部分的长．

【类型二】 平移性质的综合应用

如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移线段BE的距离，就得到此图形，下列结论正确的有(　　)

①AC∥DF；②HE＝5；③CF＝5；④阴影部分面积为.

A．1个 B．2个 C．3个 D．4个

解析：根据平移的性质得出对应点所连的线段平行且相等，对应角相等，对应线段平行且相等，阴影部分和三角形面积之间的关系，结合图形与所给的结论即可得出答案．①对应线段平行可得AC∥DF，正确；②对应线段相等可得AB＝DE＝8，则HE＝DE－DH＝8－3＝5，正确；③平移的距离CF＝BE＝5，正确；④S四边形HDFC＝S梯形ABEH＝(AB＋EH)·BE＝×(8＋5)×5＝，错误．故选C.

方法总结：本题考查平移的基本性质：①平移不改变图形的形状和大小；②对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．本题关键要找到平移的对应点．

探究点三：简单的平移作图

将如图方格中的图形向右平移4格，再向上平移2格，在方格中画出平移后的图形．

解析：按照题目要求：向右平移4格，再向上平移2格，先作各个关键点的对应点，再连接即可．

解：

方法总结：作平移图形时，找关键点的对应点是关键的一步．平移作图的一般步骤为：①确定平移的方向和距离，先确定一组对应点；②确定图形中的关键点；③利用第一组对应点和平移的性质确定图中所有关键点的对应点；④按原图形顺序依次连接对应点，所得到的图形即为平移后的图形．

三、板书设计

1．平移的定义

在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移．

2．平移的性质

一个图形和它经过平移所得的图形中，对应点所连的线段平行(或在一条直线上)且相等，对应线段平行(或在一条直线上)且相等，对应角相等．

3．简单的平移作图

教学过程中，强调学生自主探索和合作交流，学生经历将实际问题抽象成图形问题，培养学生的逻辑思维能力和空间想象能力，使得学生能将所学知识灵活运用到生活中.