作者 朷刻君

高考在考查三视图方面出题有两个方向，一是给出三视图及相关数据，求几何体的体积、表面积、内切球体积或外接球体积等；二是给出几何体，确定其中一个视图的图形．由于第二点比较简单，所以高考中考查的较少．高考中对给出三视图求相关体积、面积等的题型考查较多，一般以小题形式出现，分值为5分，该类型题的本质是考查三视图还原几何体，所以能快速准确的将三视图还原几何体，是解决这类问题的关键．

先来复习一下三视图相关的基础知识．

位置：主在上，俯在下，左在右．

大小：长对正，高平齐，宽相等．

虚实：看的见的为实线，看不见的为虚线．

本文介绍两种快速又好用的三视图还原方法．

当然，我默认大家已经掌握了基本几何体的三视图形状，这一点很重要，没有掌握的同学请自己去翻课本．

一

升点升线法

1

升点法

当主视图和侧视图的顶部都是点时，采用升点法．

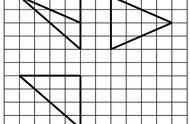
如：还原如图所示三视图的直观图．

【分析】观察三视图知主视图和侧视图的顶部都是点，则该图形可由俯视图的一个点升高形成，升的高度为主、侧视图的高2．用斜二测法画出俯视图，如下图所示．

方法总结：主、侧视图顶为点→上升点法

1．俯视画图；

2．主、侧找最高点；

3．在俯视图上将找到的点上升（上升高度为主视图的高），连接各顶点．

2

升线法

当主视图和侧视图的顶部为一点一线时，采用升线法．

例：

【分析】观察三视图知主视图和侧视图的顶部为一点一线，则该图形可由俯视图的一条线升高形成，升的高度为主、侧视图的高．用斜二测法画出俯视图，如下图所示．

方法总结：主、侧视图顶为一点一线→以点为基准升线

1．俯视画图；

2．主、侧找升高线；

3．升高直线（上升高度为主视图的高），连接对应点．

二

长方体中找点找面法

我们所学的立体图形中，有锥、柱、台、球及组合体，柱体和球的三视图还原太过简单，此处不再予以介绍．我们通过研究锥体和台体的三视图还原来介绍这种方法．

1

锥体的三视图还原

锥体的三视图的特点是三个视图中有两个三角形．也就是说，我们在看到某几何体的三视图中有两个是三角形时，即可确定该几何体为锥体，并且你要去还原它的直观图时，这两个三角形就是关键！

例：某几何体的三视图如图所示．

【分析】三视图中有三个三角形，可以确定该几何体是一个锥体，俯视图就是该锥体的底面．大家要知道，如果确定了一个锥体的底面，再确定顶点，那这个锥体就确定了．确定顶点的关键是主视图和侧视图的上顶点．

第一步：根据三视图的长、宽、高做出一个长方体，本题画出的正好是一个正方体，如图1所示．

第二步：把主视图放到立方体正对着我们的这个面上，如图2所示．

第三步：将俯视图画在立方体中，由确定的底面和顶点，连接顶点与底面的各个顶点，锥体就确定了，如下图所示．直观图还原完成．

步骤总结：

1．三视图中有两个视图为三角形，确定该几何体为锥体，余下视图作为底面．

2．将形状为三角形的视图画在对应的立方体中，根据各自上顶点的投影线找其交点，确定锥体的顶点．

3．连接各顶点，即可还原出锥体．

方法总结：两个三角形→锥体

1．确定底面；

2．确定顶点（主、侧视图上顶点的投影线交点）．

【变式训练】某几何体的三视图如图所示，还原几何体的直观图．

【提示】将侧视图作为锥体的底面，利用主视图和俯视图寻找顶点即可．

2

台体的三视图还原

台体的特点是三视图中有两个梯形，剩下的视图作为台体的下底面，还原时的关键是找上底面．

例：某几何体的三视图如图所示，还原该几何体的直观图．

【分析】首先看到该题的三视图中有两个梯形，所以可以确定该几何体是一个台体．俯视图就是该台体的一个底面．大家要知道，如果一个台体的下底面确定，再确定台体的上底面即可．上底面是由主视图和侧视图的上边决定的，下面来介绍这个上底面确定的具体方法．

第一步：根据三视图分别取长、宽、高做出一个长方体。

第二步：把主视图放到立方体正对着我们的这个面上。

步骤总结：

1．三视图中有两个视图为梯形，即可确定该几何体为台体，余下视图为该台体的下底面．

2．将形状为梯形的视图画在对应的长方体中，根据各自上边的投影面得到其相交面，确定台体的上底面．

3．连接对应顶点，即可还原台体的直观图．

方法总结：两个梯形→台体

第一步：确定下底面

第二步：确定上底面（主、侧视图的上边投影的相交面）

第三步：连接相应定点

总结

本文简单介绍了三视图还原几何体的几种简便方法，当条件满足时，这些方法非常好用．当然也还有别的方法，这里不一一介绍．三视图还原为直观图只是这类题的一个关键步骤，之后还要求其面积、体积等，就需要同学们结合各几何体的特征和已知数据求得，具体方法将在下期MOOK进行介绍．