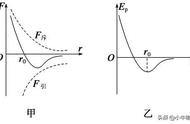
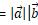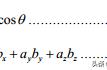关键知识点（19）：对“功”的深化。

初中时功的计算式：W=FX

X——力方向上相对于地面的位移。

高中时功的计算式：W=FXcosa

Xcosa——力方向上相对于地面的位移。

1.功是标量，但有正功、负功之分。功的正、负反映了是动力做功，还是阻力做功，动力做功为正，阻力做功为负，实质上反映了能量转化的方向，功的大小看绝对值。如：1J的功就小于一5J的功。

2.负功的两种表述：以一5J为例——负功说明这个力是阻力，可以说是阻力对物体做了一5J的功；也可以说成是物体克服这个力做了5J的功。

3.摩擦力的方向可能和物体的运动方向相同，也可能和物运动方向相反，但肯定和相对运动的方向相反，所以摩擦力可能是动力，也可能是阻力，那就说明摩擦力有可能对物体做正功，也有可能对物体做负功，也可能对物体不做功，但阻力肯定对物体做正功。

例题：质量为M的木板放在光滑的水平面上，一个质量为m的滑块（可视为质点），以某一速度沿木板上表面从木板的左端滑至右端时，两者恰好达到同样的速度而相对静止。已知木板长度为L，滑块与木板间的动摩擦因数为X，在这一过程中，木板沿水平面前进了距离l。求：

（1）摩擦力对滑块所做的功；

（2）摩擦力对木板所做的功；

（3）这一对摩擦力做功的代数和为多大？

4.作用力和反作用力对物体做功没有什么规律可循。作用力和反作用力也可能对物体都做正功；也可能对物体都做负功；也可能一个做正功，一个做负功；也可能一个做功，一个不做功。作用力和反作用力做功，各种情况都有可能，所以要具体问题具体分析。如上题中，这一对摩擦力是一对作用力和反作用力，虽然一个做正功，一个做负功，但所做功的数值不相同的。

5.总功就是物体所受的合力对物体所做的功。有两种求法：一种是先用功的计算式求出物体所受的每一个力所做的功，然后代数和求总功；另一种是先求合力，然后用功的计算式求总功。一般我们采用第一种方法求总功。

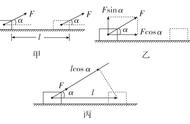
例题：一个质量为m=2Kg的物体受到与水平方向成37度角斜向上方的拉力F=10N的作用，在水平地面上移动的距离为s=2m，物体与地面之间的滑动摩擦f=4.2N。求：

（1）各个力对物体所做的功；

（2）合力对物体所做的功；

（3）各个力对物体所做的功的代数和。

6.变力功的求法。

功的计算，在中学物理中占有十分重要的地位。功的计算公式W=FXcosa，只适用于恒力做功的情况，对于变力做功，则没有一个固定公式可用，但可以通过多种方法来求变力做功。如微元法、平均值法、图像法、等效转换法等。

（1）微元法：W=FXcosa只能用来计算恒力做的功，若是求变力做的功可将运动过程分成很多小段，每一小段内的力可看作恒力，用公式w=FXcosa求出每一小段内力F所做的功，然后累加起来就得到了整个过程中变力做的功。

（2）平均值法：若变力与位移成线性关系，可通过求变力F对位移的平均值（初、末状态两个人力之和的二分之一）来计算变力的功。

（3）图像法：如图所示，在F—L图像中，若能求出图线与L轴所围的面积，则这个面积即为F在这段位移L上所做的功。类似在V—t图像中，图线和t轴所围的面积表示位移。

图象法米变力的功

（4）等效转换法:在某些情况下，通过等效转换可以将变力做功转换成恒力做功，然后可以用公式W=FXcosa求解。如图，用大小不变的力F拉绳子时，绳子对物体的拉力FT为变力，FT对物体所做的功不能用公式直接计算。但力FT对物体做的功与力F对绳子做的功相等，可将计算绳子对物体做功的问题等效转换为求力F做功的问题。

等效转换法求变力的功