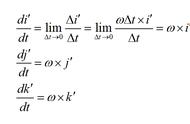则式（1）化为：

该式两边对时间t再求导，则推出当牵连运动为平动时的加速度关系：

直到这一步，我们都很容易理解。就像我们在火车里走动一样，非常容易计算我们的绝对速度和绝对加速度。但是，意外还是发生了，当牵连运动为转动时，合成加速度的公式不再适用，而变成了：

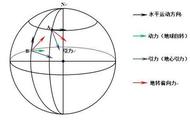
多出来的ak是什么东西，它就是我们今天的主角，学名叫科氏加速度，是由法国物理学家科里奥利于1832年在研究水轮机转动时提出的。科氏加速度出现的即突兀又难以理解，从名字上我们也很难知道它是干什么的，但是它又是如此重要，因为我们生活在地球上，很多时候参考系会选为地球，而地球是无时无刻都在旋转的，所以很多问题必须考虑科氏加速度。例如远程导弹发射后准确的落点。北半球河水向北流动时为什么右岸冲刷的比左岸剧烈。在田径比赛中，长跑项目运动员为什么都是沿着逆时针方向跑动的。这些问题的解释都离不开科氏加速度。今天我们就来认真学习一下科氏加速度是怎么产生的呢？

其实问题的关键就在于，当牵连运动为转动时，我们在对式（2）求导时，