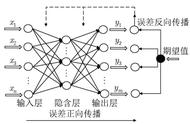
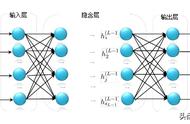
4.4 迭代

和梯度下降法类似，反向传播算法要进行多次迭代，以使得参数w和b趋向能够使损失函数最小的值。

每轮迭代时，参数w和b的变化公式如下：

这里的α是超参数：学习效率（LearningRate）。用于控制参数w和b变化的速度。

注：本文的推导只涉及一个输入样本的数据，但是在实际应用中，一般会使用批量样本，这时只需要将各个样本求得的偏导数取均值，再进行迭代即可，具体内容这里就不作展开了。

4.5 算法流程总结

简要叙述下反向传播算法的流程：

启动一个循环，事先定义好循环终止的条件，循环内容如下：

步骤1：根据公式BP1，求得神经网络模型最后一层的误差δ(L)。

步骤2：根据公式BP2，自后向前，求得神经网络模型所有层的误差δ(l)。

步骤3：根据公式BP3和BP4，求得参数w和b的偏导数∂L/∂w和∂L/∂b。

步骤4：利用偏导数∂L/∂w和∂L/∂b，更新参数w和b。

步骤5：判断当前模型的损失函数L是否符合预期，如果“是”则跳出循环终止训练，否则继续训练。

5 实操技巧

只会推公式对解决问题没有任何帮助！！！

推导数学公式的目的在于了解算法，以达到建立和优化模型的目的。所以谷歌最喜欢用的算法就是“博士生下降”（grad student descent）算法，也就是靠那些数学很好的博士去调参。。。。。。

本节介绍几个和反向传播算法相关的实操技巧。

5.1 梯度消失

先回顾一下公式BP2：

我们重点关注下激活函数的导数：

在模型刚开始学习的时候，激活函数σ的导数σ’变化得较快，这时候不会出现问题。但是，随着模型越来越逼近最优解，或者在训练的过程中不小心的一次扰动，σ’可能就等于0了。

这样，无论后一层的误差δ(l)是多少，乘上一个接近0的数，那么前一层的误差δ(l-1)自然也会近似于0。δ(l-1)一旦等于0后，那么误差就不会继续向前传播了。后续的w和b也就都等于0了。

所以，随着网络层数的增加，远离输出层（即接近输入层）的层不能够得到有效的学习，层数更深的神经网络有时反而会具有更大的训练误差。这就是梯度消失。

有时候为了预防梯度消失，我们会采用 梯度检验 的方法，以确认反向传播算法是否工作在正常状态。

5.2 激活函数的选择

我们先看看传统的sigmoid函数：