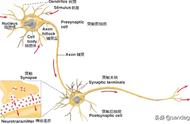
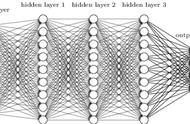
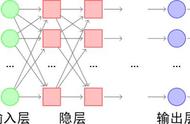
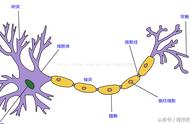
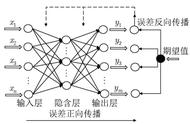
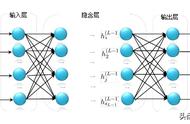
图5.1 Sigmoid函数

可以看出，Sigmoid函数只有一小段接近线性的区域，在输出趋近于0或1的区间，函数的值是保持不变或者变化很小的，反映到导数上，就是导数接近于0。

所以，我们为了避免梯度消失， 隐藏层不使用sigmoid函数作为激活函数 。

为了保证激活函数不至于那么容易就饱和，导致导数等于0，我们考虑将ReLU函数作为激活函数：

图5.2 ReLU函数和PReLU函数

在ReLU中，在自变量大于0的区间，能保证梯度不会消失，在自变量小于0的区间，函数的值被截断。在PReLU中，当x<0时，它不输出0，而是具有一个较小的斜率。

所以， 卷积神经网络钟爱的激活函数是ReLU ，它有利于反向传播阶段的计算，也能缓解过拟合。 在ReLU函数效果不好时，建议尝试PReLU函数 。此外， ReLu和PReLU一般只用于隐藏层 。

既然提到了激活函数，那么顺便列举一下其它几个Tip，虽然它们和反向传播算法无关：

激活函数最大的贡献就是将非线性引入神经网络模型，以使得算法能够学习更复杂的模型，否则即便增加网络的深度也依旧还是线性映射，起不到多层的效果。

如果是分类问题，输出层的激活函数一般会选择sigmoid函数。

在输入数据不是均值为0的正态分布时，Sigmoid函数输出的均值一般不为0，这是Sigmoid函数除了容易导致梯度消失外，另一个缺点。

5.3 参数w和b的初始化

5.3.1 参数w

在神经网络中，将权重值w初始化为0是不合适的。考虑全连接的深度神经网络，同一层中的任意神经元都是同构的，它们拥有相同的输入和输出，如果再将参数全部初始化为同样的值，那么无论前向传播还是反向传播的各个神经元的取值都将是完全相同的。

所以，我们采用 打破对称性 的方式，进行w初始值的随机化。

在使用ReLu作为激活函数时，为了避免梯度爆炸，建议w采用接近单位矩阵的初始化值。资料表明（我没验证过），初始化w为单位矩阵并使用ReLU作为激活函数，在一些应用中取得了与长短期记忆模型LSTM相似的结果。

两个比较流行的参数 w 的初始化方法：

（ 1 ） HE 初始化 (He Initialization) 。将 w 初始化为均值为 0 ，方差为 2/dim_input 的正态分布随机数。其中 dim_input 为当前层输入数据的维度。

（ 2 ） Xavier 初始化 。将 w 初始化为均值为 0 ，方差为 6/(dim_input dim_output) 的正态分布随机数。其中 dim_input 为当前层输入数据的维度， dim_output 为当前层输出数据的维度。

5.3.2 参数b

根据公式BP3：

在使用ReLU函数时，一个比较好的做法是用一个较小的正数来初始化参数b（参数b常常被初始化为1/0.1/0.01），以避免神经元节点输出为0的问题。