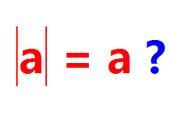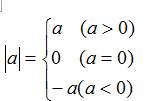绝对值符号大家都不陌生，如果问你熟不熟悉，你肯定会说很熟悉。不过老黄在教学实践中，却发现有不少学生，其实对绝对值的意义仍处在一知半解的状态中。

有很多学生对绝对值符号的理解，其实是处在“去掉数字的符号”的层面上的。这样理解是不够严谨的，不过这个不够严谨的理解，却可能可以帮学生解决一些简单的题目，比如问-3的绝对值是多少，列式是|-3|=3. 没错哦，就是把-3的符号去掉。那么|3|=3又该怎么理解呢？因为3前面没有符号，所以就不用去掉，直接取它本身嘛。

如果从“实数是由它的符号和绝对值两个部分组成的”这个角度来理解，上面的理解方式其实也是行得通的。不过如果根据下图，求a的绝对值，就有些学生会搞错了。因为在很多学生的下意识中，a的符号性质就是正的，因为很多人会写成|a|=a。这就是上面的不严谨的理解造成的。

实际上，绝对值是距离的概念。|a|表示数轴上一点到原点的距离。数轴上一点可能是正数，也可能是负数，还有可能是0，即原点本身，而距离一定不能是负数。明确了这个概率，不会根据a的符号性质去求它的绝对值了。

当a>0时，|a|=a，因为这个时候a是正数，如|3|=3；当a<0时，|a|=-a，因为这个时候a是负数，它的相反数反而是正数，如|-3|=3；当a=0时，|a|=0，因为a就是原点本身，所以距离为0。这就是初中学习的关于绝对值的知识。

不过在实际应用中，我们经常要判断两个变量的和(或差)的绝对值，比如下图中，求a b和a-b的绝对值。即求|a b|和|a-b|.

首先，|a-b|求的是a和b之间的距离，求两点的距离，就是用较大的数减去较小的数。从数轴上可以看到，b>a，因此|a-b|=b-a. 而|a b|=|a-(-b)|，即求a和-b的距离。b<0，因此-b>0>a，从而就有|a b|=-b-a.

当然，数学是一种方法论的学科，方法永远都不只一种，如果结合相反数的概念，还有其它的理解方式。不过万法归一，关键还是要理解正确，严谨，才能真正掌握数学的实质。求绝对值也是如此。

关于绝对值的知识远不止这点，一篇文章无法尽述，还要学习者自己平时多积累，归纳。高中数学，甚至是高数中，我们还有可能遇到外形和绝对值符号完全相同的符号，如求矢量的模，单元素的行列式。然而它们的内涵是存在区别的，如果不能把绝对值符号的内涵好好地理解掌握起来，以后学到这些知识的时候，就有可能造成理解的混乱了。