先来看一段描述:

PID控制器(Proportion Integration Differentiation)
俗称比例-积分-微分控制器,分别由比例单元(P)、积分单元(I)和微分单元(D)组成。一般来说,通过调整这三个单元的增益Kp,Ki和Kd来确定PID控制特性。其实PID控制器是一类控制器,而其实控制器有很多种,比如:P控制器,PI控制器,PD控制器等。

看完这段PID的描述,也许很多人就已经读不下去了,PID控制器到底和我们的现实生活有什么联系啊?怎么能让一个控制小白也很容易地理解这件事呢?
那么,让我们来举个通俗易懂的例子,帮助大家更加通俗易懂地理解PID到底是干什么的!
先讲个故事,古希腊哲学家芝诺曾提出过一条著名的悖论:阿喀琉斯是古希腊神话中十分善跑的英雄。在他和乌龟的赛跑竞赛中,他的速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。
为什么呢?因为在竞赛中,追者首先必须到达被追者的出发点,当阿喀琉斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;阿喀琉斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿喀琉斯只能再追向那个1米。
就这样,乌龟会制造出无穷个起点,它总能在起点与自己之间制造出一个距离,不管这个距离有多小,但只要乌龟不停地奋力向前爬,阿喀琉斯就永远也追不上乌龟。
看到这里大家是不是感觉到这似乎是一个死循环...
这就是鼎鼎有名的芝诺悖论!而该悖论的原理其实是一个时间问题,这里不是我们解释的重点。

▲芝诺悖论
那善跑将军阿喀琉斯就永远不会赢吗?借着这个故事,我们可以给阿喀琉斯设计一个PID控制系统,指导阿喀琉斯去追上乌龟,并且还可以一直跟随乌龟,跑过了还可以再跑回来,直到和乌龟保持同一个位置。
在这个过程中,我们相信可以凭借这个“假想”帮助大家很好地理解PID控制的原理及各参数的物理意义。
首先,还是要普及一下基础概念:
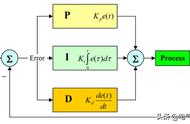
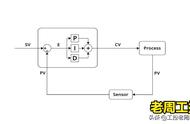
· PID控制器对反馈系统中的误差进行操作并执行以下操作
1. PID控制器计算一个与误差成比例的项- P项;
2. PID控制器计算一个与误差积分成比例的项——I项;
3. PID控制器计算一个与误差导数成比例的项——D项;
4. 这三项——P项、I项和D项——加在一起就产生了应用于被控制系统的控制信号。