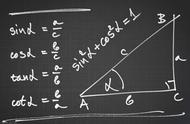
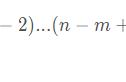④两边夹角定理：如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似，两边对应成比例且夹角相等，两三角形相似.

特别提醒：利用该判定定理时,相等的角必须是已知两组成比例边的夹角,否则两个三角形不一定相似.

例7.如图27-2-1-5,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.

求证:△ABC∽△AED.

⑤三边定理：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似，三边对应成比例，两三角形相似.

方法技巧：判断两个三角形的三边是否成比例的一般步骤:

(1) 排:将三角形的边按大小顺序排列;

(2)算:分别计算三边的比;

(3)判:由比是否相等来判断两个三角形的三边是否成比例

例8.在平面直角坐标系中,△ABC各顶点的坐标分别是A(1,2),B(1,1),C(2,0),△DEF各顶点的坐标分别是D(-1,6),E(-1,4),F(-3,2),△ABC与△DEF相似吗?请说明理由.