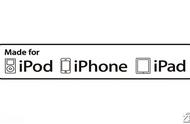
而且平行四边形面积=三角形面积=21×12÷2=126

秦九韶是怎么找到海伦数组(13，14，15)的呢？不知道，但是可以猜测一下:

若3m² 1=k² (m，n∈N)，则有

(2k-1，2k，2k 1)是海伦数组。k=7时得到海伦数组(13，14，15)。

等差海伦数组的公式

为什么痴迷于整数？

上帝创造了整数，其余的一切都是人的工作。

——克罗内克

通过对数学史的学习，我们知道了秦九韶公式的来龙去脉。

《九章算术》给出了三角形面积公式:

S=½ah (a=底，h=高)

还给出了折竹求高的勾股公式:

股弦差=勾²÷股弦和

弦=½(股弦和 股弦差)

股=½(股弦和-股弦差)

三国时期魏国数学家刘徽注解《九章算术》，又给出了另外一个公式:

股=(股弦和²-勾²)÷(2×股弦和)

刘徽和三国时期吴国数学家赵爽都证明了勾股定理。

站在前人的肩膀上，秦九韶独创三斜求积术。

吴文俊在《出入相补原理》一文中谈到了勾股定理和东西方数学，引用如下:

欧几里得《几何原本》中勾股定理的证明如下图所示，其中要先证有关三角形全等形以及三角形面积的一些定理，为此要作不少准备工作，因而在《几何原本》中直到卷一之末出现这一定理，而在整个《几何原本》中几乎没有用到。而在我国，勾股定理在《九章》中已经有多种多样的应用，成为两千来年数学发展的一个重要出发点，参阅以下各节和文末附表。

　　在东西方的古代几何体系中，勾股定理所占的地位是颇不相同的。

　　勾、股、弦和它们的和差互求

　　勾、股、弦和它们之间的和差共九个数，只须知道其中的二个就可以求得其他几个。

　　除勾、股、弦互求就是开平方之外，《九章》勾股章中有不少这方面的问题：

　　第一，知股弦差、勾，求股、弦（五题）；

　　第二，知勾股差、弦，求勾、股（一题）；

　　第三，知股弦差、勾弦差，求勾、股、弦（一题）；

　　第四，知股弦和、勾，求股、弦（一题）。

由此可见，数学发展可以大致分为三个阶段，古代数学→近代数学→现代数学。其中古代数学是常量数学，近代数学是变量数学。

在古代数学阶段，有两大数学思想主流，即西方数学的代表古希腊数学，是演绎倾向;东方数学的代表中国古代数学，是算法倾向。

可以毫不夸张的说，在明中叶之前，中国古代数学在许多数学分支领域，处于遥遥领先的地位。

但是，数学发展到近代数学阶段，中国落后了，欧洲崛起了。

数学的发展与国家的繁荣昌盛息息相关。所以，中国的近代史让人感到屈辱、辛酸和悲怆。

最后，为大家送上秦道古先生的相关资料，请看最后一个单元，本文就结束了。