为了寻求这些概念的数学表达式，物理学家们提出了一种叫做能量赝张量的东西。 （事实上，有好几种！） 现在，广义相对论以平等对待所有坐标系而自豪。 数学家发明张量正是为了满足这种需求:如果张量方程在一个坐标系中成立，那么它在所有坐标系中都成立。赝张量并不是张量(令人惊讶的是!)，仅这一点就引起了某些圈子的关注。在广义相对论中，人们必须始终防止将特定坐标系的伪影误认为真实的物理效果。(参见常见问题条目“黑洞是什么”的一些例子。)

这些赝张量有一些相当奇怪的性质。如果你选择了“错误的”坐标，即使在平坦的空时空里，它们也是非零的。通过另一种坐标选择，即使在充满重力辐射的时空中，它们也可以在任何选定的点归零。由于这些原因，大多数研究广义相对论工作的物理学家不相信赝张量给出了能量密度的一个很好的局部定义，尽管它们的积分有时作为总能量的度量是有用的。

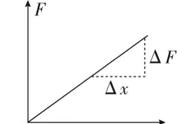
关于赝张量的另一个意见值得一提。爱因斯坦认为所有的能量都有质量，所有的质量都受重力作用。“重力能量”本身是重力的来源吗？爱因斯坦场方程是

Gμν=8πTμν.

这里Gμν是爱因斯坦张量，它编码时空曲率的信息，而Tμν是所谓的动量能量张量，我们将在下面再次讨论。 Tμν代表物质和电磁场产生的能量，但不包括“引力能”的贡献。因此，有人可能会说 ，“引力能”并不是重力的来源。另一方面，爱因斯坦场方程是非线性的；这意味着引力波相互作用(不同于麦克斯韦(线性)理论中的光波)。所以有人会说“引力能”是重力的一个来源。

在某些特殊的情况下，能量守恒的效果不那么明显。两个主要的例子是静态时空和渐近平坦时空。

让我们先看三个例子，然后再深入讨论数学公式。

非常巨大的发光物体

天文学家认识到了太阳光的红移。在准牛顿理论中，我们会说，当光爬出太阳的引力势阱时，它失去了动能，但获得了势能。广义相对论对此有不同的看法。在引力定律中，引力不是用势能来描述的，而是用时空度规来描述的。 没问题:史瓦西度规描述了一个巨大物体周围的时空，如果这个物体是球对称的，不带电荷的，并且“在宇宙中是孤独的”。史瓦西度规是静态的，也是渐近平坦的，而且能量守恒没有重大缺陷。更多细节，请查询MTW，第25章。