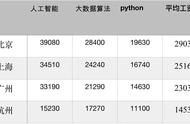
最流行的数据数学变换之一是对数变换。从本质上讲,我们只需将 log 函数应用于当前值。重要的是要注意,数据必须是正数,因此,如果您需要缩放或事先规范化数据。这种转变带来了许多好处。其中之一是数据的分布变得更加正常。反过来,这有助于我们处理偏斜的数据,并减少异常值的影响。以下是代码中的外观:
log_data = data[['body_mass_g']]
log_data['body_mass_log'] = (data['body_mass_g'] 1).transform(np.log)
log_data

如果我们检查未转换数据和转换数据的分布,我们可以看到转换后的数据更接近正态分布:

来自客户端的数据集通常很大。我们可以有数百甚至数千个功能。特别是如果我们从上面执行一些技术。大量特征可能导致过度拟合。除此之外,优化超参数和训练算法通常需要更长的时间。这就是为什么我们要从一开始就选择最相关的功能。

在功能选择方面有几种技术,但是,在本教程中,我们仅介绍最简单的一种(也是最常用的)技术 - 单变量功能选择。此方法基于单变量统计检验。它使用统计检验(如 χ2)计算输出特征对数据集中每个特征的依赖程度。在这个例子中,我们利用SelectKBest,当涉及到使用的统计测试时,它有几个选项(但是默认值是χ2,我们在这个例子中使用了那个)。以下是我们是如何做到的:
feature_sel_data = data.drop(['species'], axis=1)
feature_sel_data["island"] = feature_sel_data["island"].cat.codes
feature_sel_data["sex"] = feature_sel_data["sex"].cat.codes
# Use 3 features
selector = SelectKBest(f_classif, k=3)
selected_data = selector.fit_transform(feature_sel_data, data['species'])
selected_data
array([[ 39.1, 18.7, 181. ],
[ 39.5, 17.4, 186. ],
[ 40.3, 18. , 195. ],
...,
[ 50.4, 15.7, 222. ],
[ 45.2, 14.8, 212. ],
[ 49.9, 16.1, 213. ]])
使用超参数 k,我们定义了要从数据集中保留 3 个最有影响力的特征。此操作的输出是包含所选功能的 NumPy 数组。要使其成为pandas Dataframe,我们需要执行以下操作:
selected_features = pd.DataFrame(selector.inverse_transform(selected_data),
index=data.index,
columns=feature_sel_data.columns)
selected_columns = selected_features.columns[selected_features.var() != 0]
selected_features[selected_columns].head()