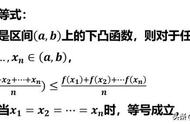琴生不等式是函数凸性的应用之一,在证明不等式中有着举足轻重的作用。
琴生不等式在高考中已算不得稀奇,好些试题都或多或少与之有着千丝万缕的关系。遗憾的是没有人愿意提出这个相对古怪的概念,但并非意味着你对此一无所知。
比如,下面就是这样的一道题。




本题考查新概念问题,涉及函数的性质、三角函数的性质、函数的最值等知识点,综合考查自学能力、迁移能力、以及应用能力,属于简单题。
是的,我知道你想说,本题的正确打开方式应该是这样:

我想,没有人会对此表示怀疑。
这里给出【法一】与【法二】,仅仅是想尝试,倘若没有琴生不等式这个前提,将会是什么样子?是否仍能求出最值?
答案是肯定的。
这里的【法一】与【法二】都用到了和差化积这个神器,我们对此并不惊异。之后便是均值不等式与导数的分道扬镳。不能说完美,但已经很满意了。
当然,在考场上还是算了吧。
夜,那么长,以数学疗人寂寞,不是修行,就是罪过。
叨叨
2019.9.18