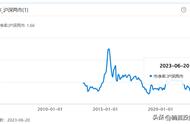
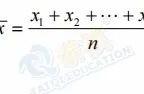在实际工作和研究中,往往只能获得数据的一部分,通常指这个数据为样本,而通过样本对整体的估计被称为假设检验。
样本是从整体中选取的较小集合,

中心极限定律:
样本的均值约等于总体的均值;
不管整体什么分布,任意一个总体的样本均值都会围绕在总体的均值周围,且呈正太分布。
关键信息:
样本的均值等于总体的均值;
样本的均值方差等于总体均值的方差除以样本数
中心极限定律就是通过样本预测整体均值的理论基础。
S= σ /√n,样本均值标准差=总体均值标准差/√样本数。
假设检验
分析思路
为了得到用户的年龄情况,
参数估计,基于用户样本数据估计整体用户年龄。
假设检验思路
根据经验或者其他方面的信息假设一个总体用户的年龄的可能值,在根据样本情况,使用工
具来验证假设是否正确。
例子:我们的用户年龄在32岁,但第三方显示该行业用户年龄为29岁,年龄相差3岁,那我
们的用户群体与该行业用户是否有显著差异?
假设检验的主要步骤
设定初始假设
初始假设:用户的平均年龄32
验证结果:接受或者拒绝这个假设
双尾检验:
默认假设=,对应假设为>或<
有2个默认拒绝假设的空间。
单尾检验:
默认≥,对应假设<
有一个拒绝默认假设的空间
计算检验的统计量
用户数80
平均年龄32
年龄标准差12
Z=(32-29)/12/√80=2.236
评估假设所用的临界值
临界值的2个因素:
假设类型、
显著性水平,判断在什么范围内的错误我们可接受,
临界值比作考试及格的分数,显著性水平是控制多少学生几个
显著性水平越底,考试难度越大,原假设难被否定
显著性水平越高,考试难度越低,原假设容易被否定
显著性水平定义区间通常为0.01-0.1之间。
在本例中:
默认假设=29
显著性水平0.05
双尾检验,概率水平均分,0.05/2=0.025
查表可知,0.025临界值为±1.96
做出决策判断
结论:Z=2.24
临界值±1.96
结论:拒绝,即我们的用户平均年龄不在29岁
实际业务中也可以用来验证两个不同样本之间的问题:
方差分析,用于两个即两个以上的样本间的显著性分析。
做出两组之间无差异的假设,且服从正态分布;
计算杨振之间平均值的差异,构建我们需要检验的统计量,Z评分。
选择合适的显著性水平,和临界值。
比较两者之间的大小,判断是否接受默认假设。
将我们看到的数据差,分解为不同组之间的差异和各个组之间的内部所产生的差异,
如果组之间的差异大到某一个特定的比例,可以认为是我们所关注的变量产生了足够大的影
响。
案例:
某店铺的裤子评分为8.6分,标准差为1,某一牛仔裤的100位用户的评分均值为9.5,这
一牛仔裤与其他裤子存在显著性差异么?
提出假设:
样本平均分数再总体评分内
计算Z评分:
Z=(9.5-8.6)/ (1/√100) = 9
选择显著性水平:
选择95%置信水平,临界值为±1.96
提示业务结论:
9 > 1.96,拒绝原假设,样本均值不在总体均值内。因此本服饰的满意度
与整体存在差异,可以研究下发生了什么。