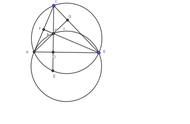
三角形的外心,指的是三角形3条边的垂直平分线交点,如下图所示。

三角形的外心
证明非常简单,只需抓住“垂直平分线上的点到两端的距离相等”,易得图中3条虚线长度均相等。因此,若以该点为圆心,虚线长度为半径作圆,则可以使三角形的3个顶点恰好位于圆上。这个圆称为三角形的外接圆,外心也因此而得名。
三角形的垂心,指的是三角形3条高的交点,如下图所示。

三角形的垂心
垂心的证明,相对来说就要难一些。其实,外心也好垂心也罢,由于相应连线均垂直于三角形的边,因此存在一定的联系,可以通过外心的存在,巧妙构造图形,从而证明垂心的存在。
过三角形的3个顶点分别作对边的平行线,可以得到一个新的三角形,如下图中红色三角形所示。

构造新三角形
易知,A、B、C恰好为红色三角形的各边中点,三角形ABC的各边恰好是红色三角形的中位线。如果过A、B、C分别作红色边的垂线,,不就能得到红色三角形的外心吗?参见下图,垂线用绿色标记。

外心和垂心的关系
聪明的你,一定看出来了,绿线交点不光是红线三角形的外心,同时也是三角形ABC的垂心!
由此可以得到结论,三角形的外心和它的中点三角形的垂心是重合的。
上述证明方法,相对于传统证法来说,显得更加巧妙,令人拍案叫绝。
数学真是奇妙,看似毫不相*东西,居然就这么联系起来了。体验数学之美,实乃学习数学的一大乐趣!